Glossary

Adjusted $R^{2}$: A method for estimating test error rate from the training error rate. Adjusted $R^{2}$ is a popular choice for comparing models with differing numbers of variables. Recall that $R^{2}$ is defined as

where TSS is the total sum of squares given by

Since the residual sum of squares always decreases given more variables, $R^{2}$ will always increase given more variables.

For a least squares fitted model with $d$ predictors, adjusted $R^{2}$ is given by

Unlike Cp, Akaike information criterion, and Bayes information criterion where a smaller value reflects lower test error, for adjusted $R^{2} ,$ a larger value signifies a lower test error.o

Maximizing adjusted $R^{2}$ is equivalent to minimizing $\frac{RSS}{n - d - 1} .$ Because $d$ appears in the denominator, the number of variables may increase or decrease the value of $\frac{RSS}{n - d - 1}$

Adjusted $R^{2}$ aims to penalize models that include unnecessary variables. This stems from the idea that after all of the correct variables have been added, adding additional noise variables will only decrease the residual sum of squares slightly. This slight decrease is counteracted by the presence of $d$ in the denominator of $\frac{RSS}{n - d - 1} .$

Agglomerative Clustering: The most common type of hierarchical clustering in which the dendrogram is built starting from the [terminal nodes][#terminal-nodes] and combining in clusters up to the trunk.

Clusters can be extracted from the dendrogram by making a horizontal cut across the dendrogram and taking the distinct sets of observations below the cut. The height of the cut to the dendrogram serves a similar role to $K$ in K-means clustering: it controls the number of clusters yielded.

Akaike Information Criterion: A method for estimating test error rate from the training error rate. The Akaike information criterion (AIC) is defined for a large class of models fit by maximum likelihood. In the case of simple linear regression, when errors follow a Gaussian distribution, maximum likelihood and least squares are the same thing, in which case, AIC is given by

This formula omits an additive constant, but even so it can be seen that Cp and AIC are proportional for least squares models and as such AIC offers no benefit in this case.

Backfitting: A method of fitting a model involving multiple parameters by repeatedly updating the fit for each predictor in turn, holding the others fixed. This approach has the benefit that each time a function is updated the fitting method for a variable can be applied to a partial residual. Backfitting can be used by generalized additive models in situations where least squares cannot be used.

A partial residual is the remainder left over after subtracting the products of the fixed variables and their respective coefficients from the response. This residual can be used as a response in a non-linear regression of the variables being updated.

For example, given a model of

a residual for $x_{i3}$ could be computed as

The yielded residual can then be used as a response in order to fit $f_{3}$ in a non linear regression on $x_{3} .$

Backward Selection: A variable selection method that begins with a model that includes all the predictors and proceeds by removing the variable with the highest p-value each iteration until some stopping condition is met. Backward selection cannot be used when $p > n .$

Backward Stepwise Selection: A variable selection method that starts with the full least squares model utilizing all $p$ predictors and iteratively removes the least useful predictor with each iteration.

An algorithm for backward stepwise selection:

1. Let $M_{p}$ denote a model using all $p$ predictors.

2. For $k = p, p - 1, ..., 1 :$
   1. Consider all $k$ models that use $k - 1$ predictors from $M_{k} .$
   2. Choose the best of these $k$ models as determined by the smallest RSS or highest $R^{2} .$ Call this model $M_{k-1} .$
3. Select the single best model from $M_{0}, ..., M_{p}$ using cross-validated prediction error, Cp (Akaike information criterion), Bayes information criterion, or adjusted $R^{2}$.

Like forward stepwise selection, backward stepwise selection searches through only $1 + \frac{p(p+1)}{2}$ models, making it useful in scenarios where $p$ is too large for best subset selection. Like forward stepwise selection, backward stepwise selection is not guaranteed to yield the best possible model.

Unlike forward stepwise selection, backward stepwise selection requires that the number of samples, $n$, is greater than the number of variables, $p ,$ so the full model with all $p$ predictors can be fit.

Both forward stepwise selection and backward stepwise selection perform a guided search over the model space and effectively consider substantially more than $1 + \frac{p(p+1)}{2}$ models.

Bagging: Bootstrap aggregation, or bagging, is a general purpose procedure for reducing the variance of statistical learning methods that is particularly useful for decision trees.

Formally, bagging aims to reduce variance by calculating $\hat{f}^{*1}(x),\ \hat{f}^{*2},\ ...,\ \hat{f}^{*B}$ using $B$ separate training sets created using bootstrap resampling, and averaging the results of the functions to obtain a single, low-variance statistical learning model given by

Bagging can improve predictions for many regression methods, but it’s especially useful for decision trees.

Bagging is applied to regression trees by constructing $B$ regression trees using $B$ bootstrapped training sets and averaging the resulting predictions. The constructed trees are grown deep and are not pruned. This means each individual tree has high variance, but low bias. Averaging the results of the $B$ trees reduces the variance.

In the case of classification trees, a similar approach can be taken, however instead of averaging the predictions, the prediction is determined by the most commonly occurring class among the $B$ predictions or the mode value.

The number of trees, $B ,$ is not a critical parameter with bagging. Picking a large value for $B$ will not lead to overfitting. Typically, a value of $B$ is chosen to ensure the variance and error rate of settled down.

Basis Function Approach: Polynomial and piecewise constant functions are special cases of a basis function approach. The basis function approach utilizes a family of functions or transformations that can be applied to a variable $X:\ b_{1}(X), b_{2}(X), ..., b_{K}(X) .$

Instead of fitting a linear model in $X ,$ a similar model that applies the fixed and known basis functions to $X$ is used:

For polynomial regression, the basis functions are $b_{j}(x) = x_{i}^{j} .$ For piecewise constant functions the basis functions are $b_{j}(x_{i}) = I(c_{j} \leq x_{i} < c_{j+1}) .$

Since the basis function model is just linear regression with predictors $b_{1}(x_{i}), b_{2}(x_{i}), ..., b_{K}(x_{i})$ least squares can be used to estimate the unknown regression coefficients. Additionally, all the inference tools for linear models like standard error for coefficient estimates and F-statistics for overall model significance can also be employed in this setting.

Many different types of basis functions exist.

Bayes Classifier: A very simple classifier that assigns each observation to the most likely class given its predictor variables.

In Bayesian terms, an observation should be classified for the predictor vector $x_{0}$ to the class $j$ for which

is largest. That is, the class for which the conditional probability that $Y=j$, given the observed predictor vector $x_{0} ,$ is largest.

Bayes Decision Boundary: The threshold inherent to a two-class Bayes classifier where the classification probability is exactly 50%.

Bayes Error Rate: The Bayes classifier yields the lowest possible test error rate since it will always choose the class with the highest probability. The Bayes error rate can be stated formally as

The Bayes error rate can also be described as the ratio of observations that lie on the “wrong” side of the decision boundary.

Bayes Information Criterion: A method for estimating test error rate from the training error rate.

For least squares models with $d$ predictors, the Bayes information criterion (BIC), excluding a few irrelevant constants, is given by

Similar to Cp, Bayes information criterion tends to take on smaller values when test MSE is low, so smaller values of BIC are preferable.

Bayes information criterion replaces the $2d\hat{\sigma}^{2}$ penalty imposed by Cp with a penalty of $log(n)d\hat{\sigma}^{2}$ where n is the number of observations. Because $log(n)$ is greater than 2 for $n > 7 ,$ the BIC statistic tends to penalize models with more variables more heavily than Cp, which in turn results in the selection of smaller models.

Bayes Theorem: Describes the probability of an event, based on prior knowledge of conditions that might be related to the event. Also known as Bayes’ law or Bayes’ rule.

Bayes’ theorem is stated mathematically as

where $A$ and $B$ are events and $P(B)$ is greater than zero.

Best Subset Selection: A variable selection method that involves fitting a separate least squares regression for each of the $2^{p}$ possible combinations of predictors and then selecting the best model.

Selecting the “best” model is not a trivial process and usually involves a two-step procedure, as outlined by the algorithm below:

1. Let $M_{0}$ denote the null model which uses no predictors and always yields the sample mean for predictions.

2. For $K = 1, 2, ..., p :$
   1. Fit all ${p \choose k}$ models that contain exactly $k$ predictors.
   2. Let $M_{k}$ denote the ${p \choose k}$ model that yields the smallest RSS or equivalently the largest $R^{2} .$
3. Select the best model from $M_{0}, ..., M_{p}$ using cross-validated prediction error, Cp (Akaike information criterion), Bayes information criterion, or adjusted $R^{2}$.

It should be noted that step 3 of the above algorithm should be performed with care because as the number of features used by the models increases, the RSS decreases monotonically and the $R^{2}$ increases monotonically. Because of this, picking the statistically best model will always yield the model involving all of the variables. This stems from the fact that RSS and $R^{2}$ are measures of training error and it’d be better to select the best model based on low test error. For this reason, step 3 utilizes cross-validated prediction error, Cp, BIC, or adjusted R^{2} to select the best models.

Best subset selection has computational limitations since $2^{p}$ models must be considered. As such, best subset selection becomes computationally infeasible for values of $p$ greater than ~40.

Bias: The error that is introduced by approximating a potentially complex function using a simple model. More flexible models tend to have less bias.

Bias-Variance Trade-Off: The relationship between bias, variance, and test mean squared error, called a trade-off because it is a challenge to find a model that has a low test mean squared error and both a low variance and a low squared bias.

Boosting: A decision tree method similar to bagging, however, where as bagging builds each tree independent of the other trees, boosting trees are grown using information from previously grown trees. Boosting also differs in that it does not use bootstrap sampling. Instead, each tree is fit to a modified version of the original data set. Like bagging, boosting combines a large number of decision trees, $\hat{f}^{*1},\ \hat{f}^{*2},\ ...,\ \hat{f}^{*B} .$

Each new tree added to a boosting model is fit to the residuals of the model instead of the response, $Y .$

Each new decision tree is then added to the fitted function to update the residuals. Each of the trees can be small with just a few terminal nodes, determined by the tuning parameter, $d .$

By repeatedly adding small trees based on the residuals, $\hat{f}$ will slowly improve in areas where it does not perform well.

Boosting has three tuning parameters:

• $B ,$ the number of trees. Unlike bagging and random forests, boosting can overfit if $B$ is too large, although overfitting tends to occur slowly if at all. Cross validation can be used to select a value for $B .$
• $\lambda ,$ the shrinkage parameter, a small positive number that controls the rate at which the boosting model learns. Typical values are $0.01$ or $0.001 ,$ depending on the problem. Very small values of $\lambda$ can require a very large value for $B$ in order to achieve good performance.
• $d ,$ the number of splits in each tree, which controls the complexity of the boosted model. Often $d=1$ works well, in which case each tree is a stump consisting of one split. This approach yields an additive model since each involves only a single variable. In general terms, $d$ is the interaction depth of the model and it controls the interaction order of the model since $d$ splits can involve at most $d$ variables.

With boosting, because each tree takes into account the trees that came before it, smaller trees are often sufficient. Smaller trees also aid interpretability.

An algorithm for boosting regression trees:

1. Set $\hat{f}(x)=0$ and $r_{i} = y_{i}$ for all $i$ in the training set.
2. For $b=1,\ b=2,\ ...,\ b=B ,$ repeat:
   1. Fit a tree $\hat{f}^{b}$ with $d$ splits ($d+1$ terminal nodes) to the training data (X, r)

   2. Update $\hat{f}$ by adding a shrunken version of the new tree:

      $$\hat{f}(x) \Leftarrow \hat{f}(x) + \lambda\hat{f}^{b}(x)$$

   3. Update the residuals:

      $$r_{i} \Leftarrow r_{i} - \lambda\hat{f}^{b}(x_{i})$$

3. Output the boosted model,

   $$\hat{f}(x) = \sum_{b=1}^{B}\lambda\hat{f}^{b}(x)$$

Bootstrap: A widely applicable resampling method that can be used to quantify the uncertainty associated with a given estimator or statistical learning approach, including those for which it is difficult to obtain a measure of variability.

The bootstrap generates distinct data sets by repeatedly sampling observations from the original data set. These generated data sets can be used to estimate variability in lieu of sampling independent data sets from the full population.

The sampling employed by the bootstrap involves randomly selecting $n$ observations with replacement, which means some observations can be selected multiple times while other observations are not included at all.

This process is repeated $B$ times to yield $B$ bootstrap data sets, $Z^{*1}, Z^{*2}, ..., Z_{*B} ,$ which can be used to estimate other quantities such as standard error.

For example, the estimated standard error of an estimated quantity $\hat{\alpha}$ can be computed using the bootstrap as follows:

Branch: A segment of a decision tree that connect two nodes.

Classification Problem: A class of problem that is well suited to statistical techniques for determining if an observation is a member of a particular class or which of a number of classes the observation belongs to.

Classification Tree: A type of decision tree that is similar to a regression tree, however it is used to predict a qualitative response. For a classification tree, predictions are made based on the notion that each observation belongs to the most commonly occurring class of the training observations in the region to which the observation belongs.

When growing a tree, the Gini index or cross-entropy are typically used to evaluate the quality of a particular split since both methods are more sensitive to node purity than classification error rate is.

When pruning a classification tree, any of the three measures can be used, though classification error rate tends to be the preferred method if the goal of the pruned tree is prediction accuracy.

Compared to linear models, decision trees will tend to do better in scenarios where the relationship between the response and the predictors is non-linear and complex. In scenarios where the relationship is well approximated by a linear model, an approach such as linear regression will tend to better exploit the linear structure and outperform decision trees.

Cluster Analysis: The task of grouping a set of observations in such a way that the observations in the same group or cluster are more similar, in some sense, to each other than those observations in other groups or clusters.

Coefficient: A number or symbol representing a number that is multiplied with a variable or an unknown quantity in an algebraic term.

Collinearity: The situation in which two or more predictor variables are closely related to one another.

Collinearity can pose problems for linear regression because it can make it hard to determine the individual impact of collinear predictors on the response.

Collinearity reduces the accuracy of the regression coefficient estimates, which in turn causes the standard error of $\beta_{j}$ to grow. Since the T-statistic for each predictor is calculated by dividing $\beta_{j}$ by its standard error, collinearity results in a decline in the true T-statistic. This may cause it to appear that $\beta_{j}$ and $x_{j}$ are related to the response when they are not. As such, collinearity reduces the effectiveness of the null hypothesis. Because of all this, it is important to address possible collinearity problems when fitting the model.

One way to detect collinearity is to generate a correlation matrix of the predictors. Any element in the matrix with a large absolute value indicates highly correlated predictors. This is not always sufficient though, as it is possible for collinearity to exist between three or more variables even if no pair of variables have high correlation. This scenario is known as multicollinearity.

Confidence Interval: A range of values such that there’s an X% likelihood that the range will contain the true, unknown value of the parameter. For example, a 95% confidence interval is a range of values such that there’s a 95% chance that the range contains the true unknown value of the parameter.

Confounding: In general, the scenario in which the result obtained with a single predictor does not match the result with multiple predictors, especially when there is correlation among the predictors. More specifically, confounding describes situations in which the experimental controls do not adequately allow for ruling out alternative explanations for the observed relationship between the predictors and the response.

Correlation: A measure of the linear relationship between $X$ and $Y ,$ calculated as

Cost Complexity Pruning: A strategy for pruning decision trees that reduces the possibility space to a sequence of trees indexed by a non-negative tuning parameter, $\alpha .$

For each value of $\alpha$ there corresponds a subtree, $T \subset T_{0} ,$ such that

where $|T|$ indicates the number of terminal nodes in the tree $T,$ $R_{m}$ is the predictor region corresponding to the mth terminal node and $\hat{y}_{R_{m}}$ is the predicted response associated with $R_{m}$ (the mean of the training observations in $R_{m} ).$

The tuning parameter $\alpha$ acts as a control on the trade-off between the subtree’s complexity and its fit to the training data. When $\alpha$ is zero, then the subtree will equal $T_{0}$ since the training fit is unaltered. As $\alpha$ increases, the penalty for having more terminal nodes increases, resulting in a smaller subtree.

As $\alpha$ increases from zero, the pruning process proceeds in a nested and predictable manner which makes it possible to obtain the whole sequence of subtrees as a function of $\alpha$ easily.

Also known as weakest link pruning.

Cp: Cp, or Mallow’s Cp, is a tool for estimating test error rate from the training error rate. For a model containing $d$ predictors fitted with least squares, the Cp estimate of test mean squared error is calculated as

where $\hat{\sigma}^{2}$ is an estimate of the variance of the error $\epsilon$ associated with each response measurement. In essence, the Cp statistic adds a penalty of $2d\hat{\sigma}^{2}$ to the training residual sum of squares to adjust for the tendency for training error to underestimate test error and adjust for additional predictors.

It can be shown that if $\hat{\sigma}^{2}$ is an unbiased estimate of $\sigma^{2}$, then Cp will be an unbiased estimate of test mean squared error. As a result, Cp tends to take on small values when test mean square error is low, so a model with a low Cp is preferable.

Cp and Akaike information criterion are proportional for least squares models and as such AIC offers no benefit over Cp in such a scenario.

Cross Entropy: Borrowed from information theory, cross-entropy can be used as a function to determine classification error rate in the context of classification trees. Formally defined as

Since $\hat{p}_{mk}$ must always be between zero and one it reasons that $\hat{p}_{mk} \mathrm{log}\ \hat{p}_{mk} \geq 0 .$ Like the Gini index, cross-entropy will take on a small value if the mth region is pure.

Cross Validation: A resampling method that can be used to estimate a given statistical methods test error or to determine the appropriate amount of flexibility.

Cross validation can be used both to estimate how well a given statistical learning procedure might perform on new data and to estimate the minimum point in the estimated test mean squared error curve, which can be useful when comparing statistical learning methods or when comparing different levels of flexibility for a single statistical learning method.

Cross validation can also be useful when $Y$ is qualitative, in which case the number of misclassified observations is used instead of mean squared error.

Curse of Dimensionality: Refers to various phenomena that arise when analyzing and organizing data in high-dimensional settings that do not occur in low-dimensional settings. The common theme of these problems is that when the dimensionality increases, the volume of the space increases so fast that the available data become sparse which can be problematic for any method that requires statistical significance because the amount of data needed to support a statistically sound and reliable result often grows exponentially with the dimensionality.

Decision Tree: A tree-like structure made from stratifying or segmenting the predictor space into a number of simple regions. These structures are referred to as trees because the splitting rules used to segment the predictor space can be summarized in a tree that is typically drawn upside down with the leaves or terminal nodes at the bottom of the tree.

Decision Tree Methods: Also known as tree-based methods. Strategies for stratifying or segmenting the predictor space into a number of simple regions. Predictions are then made using the mean or mode of the training observations in the region to which the predictions belong. These methods are referred to as trees because the splitting rules used to segment the predictor space can be summarized in a tree.

Though tree-based methods are simple and useful for interpretation, they typically aren’t competitive with the best supervised learning techniques. Because of this, approaches such as bagging, random forests, and boosting have been developed to produce multiple trees which are then combined to yield a since consensus prediction. Combining a large number of trees can often improve prediction accuracy at the cost of some loss in interpretation.

Degrees of Freedom: A numeric value that quantifies the number of values in the model that are free to vary. The degrees of freedom is a quality that summarizes the flexibility of a curve.

Dendrogram: A tree diagram, frequently used in the context of hierarchical clustering.

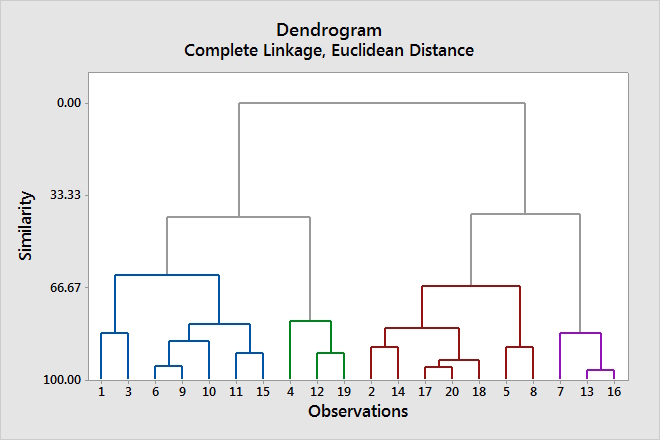
Dendrograms are attractive because a single dendrogram can be used to obtain any number of clusters.

Often people will look at the dendrogram and select a sensible number of clusters by eye, depending on the heights of the fusions and the number of clusters desired. Unfortunately, the choice of where to cut the dendrogram is not always evident.

Density Function: A function whose value for any given sample in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a relative likelihood that the value of the random variable would equal that sample.

The density function of $X$ for an observation that comes from the kth class is defined as

This means that $f_{k}(X)$ should be relatively large if there’s a high probability that an observation from the kth class features $X = x .$ Conversely, $f_{k}(X)$ will be relatively small if it is unlikely that an observation in class k would feature $X = x .$

Dimension Reduction Methods: A class of techniques that transform the predictors and then fit a least squares model using the transformed variables instead of the original predictors.

Let $Z_{1}, Z_{2}, ..., Z_{m}$ represent $M < P$ linear combinations of the original predictors, $p.$ Formally,

For some constants $\phi_{1m}, \phi_{2m}, ..., \phi_{pm}$, $m = 1, ..., M .$ It is then possible to use least squares to fit the linear regression model:

where $i=1, ..., n$ and the regression coefficients are represented by $\theta_{0}, \theta_{1}, ..., \theta_{M} .$

If the constants $\phi_{1m}, \phi_{2m}, ..., \phi_{pm}$ are chosen carefully, dimension reduction approaches can outperform least squares regression of the original predictors.

The term dimension reduction references the fact that this approach reduces the problem of estimating the $p+1$ coefficients $\theta_{0}, \theta_{1}, ..., \theta_{m} ,$ where $M < p ,$ there by reducing the dimension of the problem from $P + 1$ to $M + 1 .$

All dimension reduction methods work in two steps. First, the transformed predictors, $Z_{1}, Z_{2}, ..., Z_{M}$ are obtained. Second, the model is fit using the $M$ transformed predictors.

The difference in dimension reduction methods tends to arise from the means of deriving the transformed predictors, $Z_{1}, Z_{2}, ..., Z_{M}$ or the selection of the $\phi_{jm}$ coefficients.

Two popular forms of dimension reduction are principal component analysis and partial least squares.

Discriminant Analysis: An alternative to regression analysis applied to discrete dependent variables and concerned with separating sets of observed values into classes.

Dummy Variable: A derived variable taking on a value of 0 or 1 to indicate membership in some mutually exclusive category or class. Multiple dummy variables can be used in conjunction to model classes with more than two possible values. Similar to and often used interchangeably with the term indicator variable. Dummy variables make it easy to mix quantitative and qualitative predictors.

An example dummy variable encoding:

When dummy variables are used to model classes with more than two possible values, the number of dummy variables required will always be one less than the number of values that the predictor can take on.

For example, with a predictor that can take on three values, the following coding could be used:

F-Distribution: A continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance.

F-Statistic: A test statistic which adheres to an F-distribution under the null hypothesis which is useful to assess model fit.

The F-statistic can be computed as

where, again,

and

If the assumptions of the linear model, represented by the alternative hypothesis, are true it can be shown that

Conversely, if the null hypothesis is true, it can be shown that

This means that when there is no relationship between the response and the predictors the F-statisitic takes on a value close to $1 .$

Conversely, if the alternative hypothesis is true, then the F-statistic will take on a value greater than $1 .$

When $n$ is large, an F-statistic only slightly greater than $1$ may provide evidence against the null hypothesis. If $n$ is small, a large F-statistic is needed to reject the null hypothesis.

Forward Selection: A variable selection method that begins with a null model, a model that has an intercept but no predictors, and attempts $p$ simple linear regressions, keeping whichever predictor results in the lowest residual sum of squares. In this fashion, the predictor yielding the lowest residual sum of squares is added to the model one-by-one until some halting condition is met. Forward selection is a greedy process that may include extraneous variables.

Forward Stepwise Selection: A variable selection method that begins with a model that utilizes no predictors and successively adds predictors one-at-a-time until the model utilizes all the predictors. Specifically, the predictor that yields the greatest additional improvement is added to the model at each step.

An algorithm for forward stepwise selection is outlined below:

1. Let $M_{0}$ denote the null model that utilizes no predictors.

2. For $K = 0, 1, ..., (p - 1) :$
   1. Consider all $(p - k)$ models that augment the predictors of $M_{k}$ with one additional parameter.
   2. Choose the best $(p - k)$ model that yields the smallest RSS or largest $R^{2}$ and call it $M_{k + 1} .$
3. Select a single best model from the models, $M_{0}, M_{1}, ..., M_{p}$ using cross-validated prediction error, Cp (Akaike information criterion), Bayes information criterion, or adjusted $R^{2}$.

Forward stepwise selection involves fitting one null model and $(p - k)$ models for each iteration of $k = 0, 1, ..., (p - 1) .$ This amounts to $1 + \frac{p(p + 1)}{2}$ models which is a significant improvement over best subset selection’s $2^{p}$ models.

Forward stepwise selection may not always find the best possible model out of all $2^{p}$ models due to its additive nature. For example, forward stepwise selection could not find the best 2-variable model in a data set where the best 1-variable model utilizes a variable not used by the best 2-variable model.

Forward stepwise selection is the only variable selection method that can be applied in high-dimensional scenarios where $n < p ,$ however it can only construct submodels $M_{0}, ..., M_{n - 1}$ due to the reliance on least squares regression.

Both forward stepwise selection and backward stepwise selection perform a guided search over the model space and effectively consider substantially more than $1 + \frac{p(p+1)}{2}$ models.

Gaussian Distribution: A theoretical frequency distribution represented by a normal curve or bell curve. Also known as a normal distribution.

Generalized Additive Model: A general framework for extending a standard linear model by allowing non-linear functions of each of the predictors while maintaining additivity. Generalized additive models can be applied with both quantitative and qualitative models.

One way to extend the multiple linear regression model

to allow for non-linear relationships between each feature and the response is to replace each linear component, $\beta_{j}x_{ij} ,$ with a smooth non-linear function $f_{j}(x_{ij}) ,$ which would yield the model

This model is additive because a separate $f_{j}$ is calculated for each $x_{i}$ and then added together.

The additive nature of GAMs makes them more interpretable than some other types of models.

GAMs allow for using the many methods of fitting functions to single variables as building blocks for fitting an additive model.

Backfitting can be used by GAMs in situations where least squares cannot be used.

Gini Index: A measure of the total variance across K classes defined as

where $\hat{p}_{mk}$ represents the proportion of the training observations in the mth region that are from the kth class.

The Gini index can be viewed as a measure of region purity as a small value indicates the region contains mostly observations from a single class.

Often used as a function for assessing classification error rate in the context of classification trees.

Heteroscedasticity: A characteristic of a collection of random variables in which there are sub-populations that have different variability from other sub-populations. Heteroscedasticity can lead to regression models that seem stronger than they really are since standard errors, confidence intervals, and hypothesis testing all assume that error terms have a constant variance.

Hierarchical Clustering: A clustering method that generates clusters by first building a dendrogram then obtains clusters by cutting the dendrogram at a height that will yield a desirable set of clusters.

The hierarchical clustering dendrogram is obtained by first selecting some sort of measure of dissimilarity between the each pair of observations; often Euclidean distance is used. Starting at the bottom of the dendrogram, each of the $n$ observations is treated as its own cluster. With each iteration, the two clusters that are most similar are merged together so there are $n - 1$ clusters. This process is repeated until all the observations belong to a single cluster and the dendrogram is complete.

The dissimilarity between the two clusters that are merged indicates the height in the dendrogram at which the fusion should be placed.

One issue not addressed is how clusters with multiple observations are compared. This requires extending the notion of dissimilarity to a pair of groups of observations. Linkage defines the dissimilarity between two groups of observations.

The term hierarchical refers to the fact that the clusters obtained by cutting the dendrogram at the given height are necessarily nested within the clusters obtained by cutting the dendrogram at any greater height.

The hierarchical structure assumption is not always valid. For example, splitting a group of people in to sexes and splitting a group of people by race yield clusters that aren’t necessarily hierarchical in structure. Because of this, hierarchical clustering can sometimes yield worse results than K-means clustering.

Hierarchical Principle: A guiding philosophy that states that, when an interaction term is included in the model, the main effects should also be included, even if the p-values associated with their coefficients are not significant. The reason for this is that $X_{1}X_{2}$ is often correlated with $X_{1}$ and $X_{2}$ and removing them tends to change the meaning of the interaction.

If $X_{1}X_{2}$ is related to the response, then whether or not the coefficient estimates of $X_{1}$ or $X_{2}$ are exactly zero is of limited interest.

High-Dimensional: A term used to describe scenarios where there are more features than observations.

High Leverage: In contrast to outliers which relate to observations for which the response $y_{i}$ is unusual given the predictor $x_{i}$, observations with high leverage are those that have an unusual value for the predictor $x_{i}$ for the given response $y_{i} .$

High leverage observations tend to have a sizable impact on the estimated regression line and as a result, removing them can yield improvements in model fit.

For simple linear regression, high leverage observations can be identified as those for which the predictor value is outside the normal range. With multiple regression, it is possible to have an observation for which each individual predictor’s values are well within the expected range, but that is unusual in terms of the combination of the full set of predictors.

To qualify an observation’s leverage, the leverage statistic can be computed.

A large leverage statistic indicates an observation with high leverage.

For simple linear regression, the leverage statistic can be computed as

The leverage statistic always falls between $\frac{1}{n}$ and $1$ and the average leverage is always equal to $\frac{p + 1}{n} .$ So, if an observation has a leverage statistic greatly exceeds $\frac{p + 1}{n}$ then it may be evidence that the corresponding point has high leverage.

Hybrid Subset Selection: Hybrid subset selection methods add variables to the model sequentially, analogous to forward stepwise selection, but with each iteration they may also remove any variables that no longer offer any improvement to model fit.

Hybrid approaches try to better simulate best subset selection while maintaining the computational advantages of stepwise approaches.

Hyperplane: In a $p$-dimensional space, a hyperplane is a flat affine subspace of dimension $p - 1 .$ For example, in two dimensions, a hyperplane is a flat one-dimensional subspace, or in other words, a line. In three dimensions, a hyperplane is a plane.

The word affine indicates that the subspace need not pass through the origin.

A $p$-dimensional hyperplane is defined as

which means that any $X = (X_{1},\ X_{2},\ ...,\ X_{p})^{T}$ for which the above hyperplane equation holds is a point on the hyperplane.

If $X = (X_{1},\ X_{2},\ ...,\ X_{p})^{T}$ doesn’t fall on the hyperplane, then it must fall on one side of the hyperplane or the other. As such, a hyperplane can be thought of as dividing a $p$-dimensional space into two partitions. Which side of the hyperplane a point falls on can be computed by calculating the sign of the result of plugging the point into the hyperplane equation.

Hypothesis Testing: The process of applying the scientific method to produce, test, and iterate on theories. Typical steps include: making an initial assumption; collecting evidence (data); and deciding whether to accept or reject the initial assumption, based on the available evidence (data).

Input: The variables that contribute to the value of the response or dependent variable in a given function. Also known as predictors, independent variables, or features. Input variables may be qualitative or quantitative.

Indicator Variable: A derived variable taking on a mutually exclusive value of 0 or 1 based on an associated indicator function which typically returns 0 to indicate the absence of some property and 1 to indicate the presence of that property. Similar to and often used interchangeably with the term dummy variable, especially when dealing with classes with only two possible values. Indicator variables make it easy to mix qualitative and quantitative predictors.

An example indicator variable encoding:

Interaction Term: A derived predictor that gets its value from computing the product of two associated predictors with the goal of better capturing the interaction between the two given predictors.

A simple linear regression model account for interaction between the predictors would look like

where $\beta_{3}$ can be interpreted as the increase in effectiveness of $\beta_{1}$ given a one-unit increase in $\beta_{2}$ and vice-versa.

It is sometimes possible for an interaction term to have a very small p-value while the associated main effects, $X_{1}, X_{2}, etc.$, do not. Even in such a scenario the main effects should still be included in the model due to the hierarchical principle.

Intercept: In a linear model, the value of the dependent variable, $Y ,$ when the independent variable, $X ,$ is equal to zero. Also described as the point at which a given line intersects with the x-axis.

Inner Node: One of the many points in a decision tree where the predictor space is split. Also known as inner node, or inode for short, or branch node.

Irreducible Error: A random error term that is independent of the independent variables with a mean roughly equal to zero that is intended to account for inaccuracies in a function which may arise from unmeasured variables or unmeasured variation. The irreducible error will always enforce an upper bound on the accuracy of attempts to predict the dependent variable.

K-Fold Cross Validation: A resampling method that operates by randomly dividing the set of observations into $K$ groups or folds of roughly equal size. Similar to leave-one-out cross validation, each of the $K$ folds is used as the validation set while the other $K - 1$ folds are used as the test set to generate $K$ estimates of the test error. The K-fold cross validation estimated test error comes from the average of these estimates.

It can be shown that leave-one-out cross validation is a special case of K-fold cross validation where $K = n .$

Typical values for $K$ are 5 or 10 since these values require less computation than when $K$ is equal to $n .$

There is a bias-variance trade-off inherent to the choice of $K$ in K-fold cross validation. Typically, values of $K = 5$ or $K = 10$ are used as these values have been empirically shown to produce test error rate estimates that suffer from neither excessively high bias nor very high variance.

In terms of bias, leave-one-out cross validation is preferable to K-fold cross validation and K-fold cross validation is preferable to the validation set approach.

In terms of variance, K-fold cross validation where $K < n$ is preferable to leave-one-out cross validation and leave-one-out cross validation is preferable to the validation set approach.

K-Means Clustering: A method of cluster analysis that aims to partition a data set into $K$ distinct, non-overlapping clusters, where $K$ is stipulated in advance.

The K-means clustering procedure is built on a few constraints. Given sets containing the indices of the observations in each cluster, $C_{1},\ \dots, C_{K} ,$ these sets must satisfy two properties:

1. Each observation belongs to at least one of the $K$ clusters: $\normalsize C_{1} \cup C_{2} \cup \dots \cup C_{K} = \{1,\ \dots,\ n\}$
2. No observation belongs to more than one cluster. Clusters are non-overlapping. $\normalsize C_{k} \cap C_{k^{\prime}} = \{\}\ \mathrm{for\ all\ k,}\ k \neq k^{\prime}$

In the context of K-means clustering, a good cluster is one for which the within-cluster variation is as small as possible. For a cluster $C_{k} ,$ the within-cluster variation, $W(C_{k}) ,$ is a measure of the amount by which the observations in a cluster differ from each other. As such, an ideal cluster would minimize

Informally, this means that the observations should be partitioned into $K$ clusters such that the total within-cluster variation, summed over all $K$ clusters, is as small as possible.

In order to solve this optimization problem, it is first necessary to define the means by which within-cluster variation will be evaluated. There are many ways to evaluate within-cluster variation, but the most common choice tends to be squared Euclidean distance, defined as

where $\\| C_{k}$ $\\|$ denotes the number of observations in the kth cluster.

Combined with the abstract optimization problem outlined earlier yields

Finding the optimal solution to this problem is computationally infeasible unless $K$ and $n$ are very small, since there are almost $K^{n}$ ways to partition $n$ observations into $K$ clusters. However, a simple algorithm exists to find a local optimum.

K-means clustering gets its name from the fact that the cluster centroids are computed as means of the observations assigned to each cluster.

K-Nearest Neighbors Classifier: A classifier that takes a positive integer $K$ and first identifies the $K$ points that are nearest to $x_{0} ,$ represented by $N_{0} .$ It next estimates the conditional probability for class $j$ based on the fraction of points in $N_{0}$ that have a response equal to $j .$ Formally, the estimated conditional probability can be stated as

The K-Nearest Neighbor classifier then applies Bayes theorem and yields the classification with the highest probability.

Despite its simplicity, the K-Nearest Neighbor classifier often yields results that are surprisingly close to the optimal Bayes classifier.

The choice of $K$ can have a drastic effect on the yielded classifier, as $K$ controls the bias-variance trade-off for the classifier.

K-Nearest Neighbors Regression: A non-parametric method akin to linear regression.

Given a value for $K$ and a prediction point $x_{0}$, k-nearest neighbors regression first identifies the $K$ observations that are closest to $x_{0}$, represented by $N_{0} .$ $f(x_{0})$ is then estimated using the average of $N_{0i}$ like so

In higher dimensions, K-nearest neighbors regression often performs worse than linear regression. This is often due to combining too small an $n$ with too large a $p$, resulting in a given observation having no nearby neighbors. This is often called the curse of dimensionality.

Knot: For regression splines, one of the $K$ points at which the coefficients utilized by the underlying function are changed to better model the respective region.

There are a variety of methods for choosing the number and location of the knots. Because the regression spline is most flexible in regions that contain a lot of knots, one option is to place more knots where the function might vary the most and fewer knots where the function might be more stable. Another common practice is to place the knots in a uniform fashion. One means of doing this is to choose the desired degrees of freedom and then use software or other heuristics to place the corresponding number of knots at uniform quantiles of the data.

Cross validation is a useful mechanism for determining the appropriate number of knots and/or degrees of freedom.

$\ell_{1}$ norm: The $\ell_{1}$ norm of a vector is defined as

$\ell_{2}$ norm: The $\ell_{2}$ norm of a vector is defined as

The $\ell_{2}$ norm measures the distance of the vector, $\beta ,$ from zero.

Lasso: A more recent alternative to ridge regression that allows for excluding some variables.

Coefficient estimates for the lasso are generated by minimizing the quantity

The main difference between ridge regression and the lasso is the change in penalty. Instead of the $\beta_{j}^{2}$ term of ridge regression, the lasso uses the $\ell_{1}$ norm of the coefficient vector $\beta$ as its penalty term. The $\ell_{1}$ norm of a coefficient vector $\beta$ is given by

The $\ell_{1}$ penalty can force some coefficient estimates to zero when the tuning parameter $\lambda$ is sufficiently large. This means that like subset methods, the lasso performs variable selection. This results in models generated from the lasso tending to be easier to interpret the models formulated with ridge regression. These models are sometimes called sparse models since they include only a subset of the variables.

The variable selection of the lasso can be considered a kind of soft thresholding. The lasso will perform better in scenarios where not all of the predictors are related to the response, or where some number of variables are only weakly associated with the response.

Least Squares Line: The line yielded by least squares regression,

where the coefficients $\hat{\beta_{0}}$ and $\hat{\beta_{1}}$ are approximations of the unknown coefficients of the population regression line, $\beta_{0}$ and $\beta_{1} .$

Leave-One-Out Cross Validation: A resampling method similar to the validation set approach, except instead of splitting the observations evenly, leave-one-out cross-validation withholds only a single observation for the validation set. This process can be repeated $n$ times with each observation being withheld once. This yields $n$ mean squared errors which can be averaged together to yield the leave-one-out cross-validation estimate of the test mean squared error.

Leave-one-out cross validation has much less bias than the validation set approach. Leave-one-out cross validation also tends not to overestimate the test mean squared error since many more observations are used for training. In addition, leave-one-out cross validation is much less variable, in fact, it always yields the same result since there’s no randomness in the set splits.

Leave-one-out cross validation can be expensive to implement since the model has to be fit $n$ times. This can be especially expensive in situations where $n$ is very large and/or when each individual model is slow to fit.

In the classification setting, the leave-one-out cross validation error rate takes the form

where $Err_{i} = I(y \neq \hat{y}_{i}) .$ The K-fold cross validation error rate and the validation set error rate are defined similarly.

Likelihood Function: A function often used to estimate parameters from a set of independent observations. For logistic regression a common likelihood function takes the form

Estimates for $\beta_{0}$ and $\beta_{1}$ are chosen so as to maximize this likelihood function for logistic regression.

Linear Discriminant Analysis: While logistic regression models the conditional distribution of the response $Y$ given the predictor(s) $X ,$ linear discriminant analysis takes the approach of modeling the distribution of the predictor(s) $X$ separately in each of the response classes , $Y$, and then uses Bayes’ theorem to invert these probabilities to estimate the conditional distribution.

Linear discriminant analysis is popular when there are more than two response classes. Beyond its popularity, linear discriminant analysis also benefits from not being susceptible to some of the problems that logistic regression suffers from:

• The parameter estimates for logistic regression can be surprisingly unstable when the response classes are well separated. Linear discriminant analysis does not suffer from this problem.
• Logistic regression is more unstable than linear discriminant analysis when $n$ is small and the distribution of the predictors $X$ is approximately normal in each of the response classes.

Linkage: A measure of the dissimilarity between two groups of observations.

There are four common types of linkage: complete, average, single, and centroid. Average, complete and single linkage are most popular among statisticians. Centroid linkage is often used in genomics. Average and complete linkage tend to be preferred because they tend to yield more balanced dendrograms. Centroid linkage suffers from a major drawback in that an inversion can occur where two clusters fuse at a height below either of the individual clusters in the dendrogram.

Complete linkage uses the maximal inter-cluster dissimilarity, calculated by computing all of the pairwise dissimilarities between observations in cluster A and observations in cluster B and taking the largest of those dissimilarities.

Single linkage uses the minimal inter-cluster dissimilarity given by computing all the pairwise dissimilarities between observations in clusters A and B and taking the smallest of those dissimilarities. Single linkage can result in extended trailing clusters where each observation fuses one-at-a-time.

Average linkage uses the mean inter-cluster dissimilarity given by computing all pairwise dissimilarities between the observations in cluster A and the observations in cluster B and taking the average of those dissimilarities.

Centroid linkage computes the dissimilarity between the centroid for cluster and A and the centroid for cluster B.

Local Regression: An approach to fitting flexible non-linear functions which involves computing the fit at a target point $x_{0}$ using only the nearby training observations.

Each new point from which a local regression fit is calculated requires fitting a new weighted least squares regression model by minimizing the appropriate regression weighting function for a new set of weights.

Log-Odds: Taking a logarithm of both sides of the logistic odds equation yields an equation for the log-odds or logit,

Logistic regression has log-odds that are linear in terms of $X .$

The log-odds equation for multiple logistic regression can be expressed as

Logistic Function: A function with a common “S” shaped Sigmoid curve guaranteed to return a value between $0$ and $1$. For logistic regression, the logistic function takes the form

Logistic Regression: A regression model where the dependent variable is categorical or qualitative. Logistic regression models the probability that $y$ belongs to a particular category rather than modeling the response itself. Logistic regression uses a logistic function to ensure a prediction between $0$ and $1 .$

Logit: Taking a logarithm of both sides of the logistic odds equation yields an equation for the log-odds or logit.

Logistic regression has log-odds that are linear in terms of $X .$

Maximal Margin Classifier: A classifier that uses the maximal margin hyperplane to classify test observations. The maximal margin hyperplane (also known as the optimal separating hyperplane) is the separating hyperplane which has the farthest minimum distance, or margin, from the training observations in terms of perpendicular distance.

The maximal margin classifier classifies a test observation $x^{*}$ based on the sign of

where $\beta_{0},\ \beta_{1},\ \dots,\ \beta_{p}$ are the coefficients of the maximal margin hyperplane.

The maximal margin hyperplane represents the mid-line of the widest gap between the two classes.

If no separating hyperplane exists, no maximal margin hyperplane exists either. However, a soft margin can be used to construct a hyperplane that almost separates the classes. This generalization of the maximal margin classifier is known as the support vector classifier.

Maximum Likelihood: A strategy utilized by logistic regression to estimate regression coefficients.

Maximum likelihood plays out like so: determine estimates for $\beta_{0}$ and $\beta_{1}$ such that the predicted probability of $\hat{p}(x_{i})$ corresponds with the observed classes as closely as possible. Formally, this yield an equation called a likelihood function:

Estimates for $\beta_{0}$ and $\beta_{1}$ are chosen so as to maximize this likelihood function.

Linear regression’s least squares approach is actually a special case of maximum likelihood.

Maximum likelihood is also used to estimate $\beta_{0}, \beta_{1}, \ldots, \beta_{p}$ in the case of multiple logistic regression.

Mean Squared Error: A statistical method for assessing how well the responses predicted by a modeled function correspond to the actual observed responses. Mean squared error is calculated by calculating the average squared difference between the predicted responses and their relative observed responses, formally,

Mean squared error will be small when the predicted responses are close to the true responses and large if there’s a substantial difference between the predicted response and the observed response for some observations.

Mixed Selection: A variable selection method that begins with a null model, like forward selection, repeatedly adding whichever predictor yields the best fit. As more predictors are added, the p-values become larger. When this happens, if the p-value for one of the variables exceeds a certain threshold, that variable is removed from the model. The selection process continues in this forward and backward manner until all the variables in the model have sufficiently low p-values and all the predictors excluded from the model would result in a high p-value if added to the model.

Model Assessment: The process of evaluating the performance of a given model.

Model Selection: The process of selecting the appropriate level of flexibility for a given model.

Multicollinearity: The situation in which collinearity exists between three or more variables even if no pair of variables have high correlation.

Multicollinearity can be detected by computing the [variance inflation factor][variance-inflation-factor].

Multiple Linear Regression: An extension of simple linear regression that accommodates multiple predictors.

The multiple linear regression model takes the form of

$X_{j}$ represents the $j \text{th}$ predictor and $\beta_{j}$ represents the average effect of a one-unit increase in $X_{j}$ on $Y$, holding all other predictors fixed.

Multiple Logistic Regression: An extension of simple logistic regression that accommodates multiple predictors. Multiple logistic regression can be generalized as

where $X = (X_{1}, X_{2}, \ldots, X_{p})$ are $p$ predictors.

Multivariate Gaussian Distribution: A generalization of the one-dimensional Gaussian distribution that assumes that each predictor follows a one-dimensional normal distribution with some correlation between the predictors. The more correlation between predictors, the more the bell shape of the normal distribution will be distorted.

A p-dimensional variable X can be indicated to have a multivariate Gaussian distribution with the notation $X \sim N(\mu, \Sigma)$ where $E(x) = \mu$ is the mean of $X$ (a vector with p components) and $\mathrm{Cov}(X) = \Sigma$ is the p x p covariance matrix of $X$.

Multivariate Gaussian density is formally defined as

Natural Spline: A regression spline with additional boundary constraints that force the function to be linear in the boundary region.

Non-Parametric: Not involving any assumptions about the form or parameters of a function being modeled.

Non-Parametric Methods: A class of techniques that don’t make explicit assumptions about the shape of the function being modeled and instead seek to estimate the function by getting as close to the training data points as possible without being too coarse or granular, preferring smoothness instead. Non-parametric methods can fit a wider range of possible functions since essentially no assumptions are made about the form of the function being modeled.

Normal Distribution: A theoretical frequency distribution represented by a normal curve or bell curve. Also known as a Gaussian distribution.

Null Hypothesis: The most common hypothesis test involves testing the null hypothesis that states

$H_{0}$: There is no relationship between $X$ and $Y$

versus the alternative hypothesis

$H_{1}$: Thee is some relationship between $X$ and $Y .$

In mathematical terms, the null hypothesis corresponds to testing if $\beta_{1} = 0$, which reduces to

which evidences that $X$ is not related to $Y .$

To test the null hypothesis, it is necessary to determine whether the estimate of $\beta_{1}$, $\hat{\beta_{1}}$, is sufficiently far from zero to provide confidence that $\beta_{1}$ is non-zero.

Null Model: In linear regression, a model that includes an intercept, but no predictors.

Odds: The logistic function can be rebalanced to yield

$\frac{p(X)}{1 - p(X)}$ is known as the odds and takes on a value between $0$ and infinity.

As an example, a probability of 1 in 5 yields odds of $\frac{1}{4}$ since $\frac {0.2}{1 - 0.2} = \frac{1}{4} .$

Outlier: A point for which $y_{i}$ is far from the value predicted by the model.

Excluding outliers can result in improved residual standard error and improved $\mathrm{R}^{2}$ values, usually with negligible impact to the least squares fit.

Residual plots can help identify outliers, though it can be difficult to know how big a residual needs to be before considering a point an outlier. To address this, it can be useful to plot the studentized residuals instead of the normal residuals. Observations whose studentized residual is greater than $|3|$ are possible outliers.

Outliers should only be removed when confident that the outliers are due to a recording or data collection error since outliers may otherwise indicate a missing predictor or other deficiency in the model.

One-Standard-Error Rule: The one-standard-error rule advises that when many models have low estimated test error and it’s difficult or variable as to which model has the lowest test error, one should select the model with the fewest variables that is within one standard error of the lowest estimated test error. The rationale being that given a set of more or less equally good models, it’s often better to pick the simpler model.

One-Versus-All: Assuming $K > 2 ,$ [one-versus-all][glossary-one-versus-all] fits $K$ SVMs, each time comparing one of the $K$ classes to the remaining $K - 1$ classes. Assuming a test observation $x^{*}$ and coefficients $\beta_{0k},\ \beta_{1k},\ \dots,\ \beta_{pk}$, resulting from fitting an SVM comparing the kth class (coded as $+1$) to the others (coded as $-1$), the test observation is assigned to the class for which

is largest, as this amounts to the highest level of confidence.

One-Versus-One: Assuming $K > 2 ,$ [one-versus-one][glossary-one-versus-one], or all-pairs, constructs $K \choose 2$ SVMs, each of which compares a pair of classes. A test observation would be classified using each of the $K \choose 2$ classifiers, with the final classification given by the class most frequently predicted by the $K \choose 2$ classifiers.

Output: The result of computing a given function with all of the independent variables replaced with concrete values. Also known as the response or dependent variable. Output may be qualitative or quantitative.

Overfitting: A phenomenon where a model closely matches the training data such that it captures too much of the noise or error in the data. This results in a model that fits the training data very well, but doesn’t make good predictions under test or in general. Overfitting refers specifically to scenarios in which a less flexible model would have yielded a smaller test mean squared error.

P-Value: When the null hypothesis is true, the probability for a given model that a statistical summary (such as a t-statistic) would be of equal or of greater magnitude compared to the actual observed results. Can indicate an association between the predictor and the response if the value is sufficiently small, further indicating that the null hypothesis may not be true.

Parameter: A number or symbol representing a number that is multiplied with a variable or an unknown quantity in an algebraic term.

Parametric: Relating to or expressed in terms of one or more parameters.

Parametric Methods: A class of techniques that make explicit assumptions about the shape of the function being modeled and seek to estimate the assumed function by estimating parameters or coefficients that yield a function that fits the training data points as closely as possible, within the constraints of the assumed functional form. Parametric methods tend to have higher bias since they make assumptions about the form of the function being modeled.

Partial Least Squares: A regression technique that first identifies a new set of features $Z_{1}, ..., Z_{M}$ that are linear combinations of the original predictors and then uses these $M$ new features to fit a linear model using least squares.

Unlike principal component regression, partial least squares makes use of the response $Y$ to identify new features that not only approximate the original predictors well, but that are also related to the response.

In practice, partial least squares often performs no better than principal component regression or ridge regression. Though the supervised dimension reduction of partial least squares can reduce bias, it also has the potential to increase variance. Because of this, the benefit of partial least squares compared to principal component regression is often negligible.

Piecewise Constant Function:

Polynomial Regression: An extension to the linear model intended to accommodate non-linear relationships and mitigate the effects of the linear assumption by incorporating polynomial functions of the predictors into the linear regression model.

For example, in a scenario where a quadratic relationship seems likely, the following model could be used

Population Regression Line: The line that describes the best linear approximation to the true relationship between $X$ and $Y$ for the population.

Portion of Variance Explained: A means of determining how much of the variance in the data is not captured by the first $M$ principal components.

The total variance in the data set assuming the variables have been centered to have a mean of zero is defined by

The variance explained by the mth principal component is defined as

From these equations it can be seen that the portion of the variance explained for the mth principal component is given by

To compute the cumulative portion of variance explained by the first $m$ principal components, the individual portions should be summed. In total there are $\mathrm{Min}(n-1,\ p)$ principal components and their portion of variance explained sums to one.

Posterior Probability: Taking into account the predictor value for a given observation, the probability that the observation belongs to the kth class of a qualitative variable $Y$ that can take on $K \geq 2$ distinct, unordered values. More formally,

Prediction Interval: A measure of confidence in the prediction of an individual response, $y = f(x) + \epsilon .$ Prediction intervals will always be wider than confidence intervals because they take into account the uncertainty associated with $\epsilon$, the irreducible error.

Principal Component Analysis: A technique for reducing the dimension of an $n \times p$ data matrix $X$ to derive a low-dimensional set of features from a large set of variables.

The first principal component direction of the data is the line along which the observations vary the most.

Put another way, the first principal component direction is the line such that if the observations were projected onto the line then the projected observations would have the largest possible variance and projecting observations onto any other line would yield projected observations with lower variance.

Another interpretation of principal component analysis describes the first principal component vector as the line that is as close as possible to the data. In other words, the first principal component line minimizes the sum of the squared perpendicular distances between each point and the line. This means that the first principal component is chosen such that the projected observations are as close as possible to the original observations.

Projecting a point onto a line simply involves finding the location on the line which is closest to the point.

As many as $\mathrm{Min}(n-1, p)$ principal components can be computed.

Principal Component Regression: A regression method that first constructs the first $M$ principal components, $Z_{1}, Z_{2}, ..., Z_{M} ,$ and then uses the components as the predictors in a linear regression model that is fit with least squares.

The premise behind this approach is that a small number of principal components can often suffice to explain most of the variability in the data as well as the relationship between the predictors and the response. This relies on the assumption that the directions in which $X_{1}, ..., X_{p}$ show the most variation are the directions that are associated with the predictor $Y .$ Though not always true, it is true often enough to approximate good results.

Prior Probability: The probability that a given observation is associated with the kth class of a qualitative variable $Y$ that can take on $K \geq 2$ distinct, unordered values.

Quadratic Discriminant Analysis: An alternative approach to linear discriminant analysis that makes most of the same assumptions, except that quadratic discriminant analysis assumes that each class has its own covariance matrix. This amounts to assuming that an observation from the kth class has a distribution of the form

where $\Sigma_{k}$ is a covariance matrix for class $k$.

This yields a Bayes classifier that assigns an observation $X = x$ to the class with the largest value for

which is equivalent to

The quadratic discriminant analysis Bayes classifier gets its name from the fact that it is a quadratic function in terms of $x .$

Qualitative Value: A value expressed or expressible as a quality, typically limited to one of K different classes or categories.

Quantitative Value: A value expressed or expressible as a numerical quantity.

$R^{2}$ Statistic: A ratio capturing the proportion of variance explained as a value between $0$ and $1$, independent of the unit of $Y .$

To calculate the $R^2$ statistic, the following formula may be used

where RSS is the residual sum of squares,

and TSS is the total sum of squares,

An $R^{2}$ statistic close to $1$ indicates that a large portion of the variability in the response is explained by the model. An $R^{2}$ value near $0$ indicates that the model accounted for very little of the variability of the model.

An $R^{2}$ value near $0$ may occur because the type of model is wrong and/or because the inherent $\sigma^{2}$ is high.

Random Forest: Random forests are similar to bagged trees, however, random forests introduce a randomized process that helps decorrelate trees.

During the random forest tree construction process, each time a split in a tree is considered, a random sample of $m$ predictors is chosen from the full set of $p$ predictors to be used as candidates for making the split. Only the randomly selected $m$ predictors can be considered for splitting the tree in that iteration. A fresh sample of $m$ predictors is considered at each split. Typically $m \approx \sqrt{p}$ meaning that the number of predictors considered at each split is approximately equal to the square root of the total number of predictors, $p .$ This means that at each split only a minority of the available predictors are considered. This process helps mitigate the strength of very strong predictors, allowing more variation in the bagged trees, which ultimately helps reduce correlation between trees and better reduces variance. In the presence of an overly strong predictor, bagging may not outperform a single tree. A random forest would tend to do better in such a scenario.

On average, $\frac{p - m}{p}$ of the splits in a random forest will not even consider the strong predictor which causes the resulting trees to be less correlated. This process is a kind of decorrelation process.

As with bagging, random forests will not overfit as $B$ is increased, so a value of $B$ should be selected that allows the error rate to settle down.

Recursive Binary Splitting: A top-down approach that begins at the top of a decision-tree where all the observations belong to a single region, and successively splits the predictor space into two new branches. Recursive binary splitting is greedy strategy because at each step in the process the best split is made relative to that particular step rather than looking ahead and picking a split that will result in a better split at some future step.

At each step the predictor $X_{j}$ and the cutpoint $s$ are selected such that splitting the predictor space into regions $\{X|X_{j} < s\}$ and $\{X|X_{j} \geq s\}$ leads to the greatest possible reduction in the residual sum of squares. This means that at each step, all the predictors $X_{1},\ X_{2},\ ...,\ X_{j}$ and all possible values of the cutpoint $s$ for each of the predictors are considered. The optimal predictor and cutpoint are selected such that the resulting tree has the lowest residual sum of squares compared to the other candidate predictors and cutpoints.

More specifically, for any $j$ and $s$ that define the half planes

and

the goal is to find the $j$ and $s$ that minimize the equation

where $\hat{y}_{R_{1}}$ and $\hat{y}_{R_{2}}$ are the mean responses for the training observations in the respective regions.

Only one region is split each iteration. The process concludes when some halting criteria are met.

This process can result in overly complex trees that overfit the data leading to poor test performance. A smaller tree often leads to lower variance and better interpretation at the cost of a little bias.

Regression Problem: A class of problem that is well suited to statistical techniques for predicting the value of a dependent variable or response by modeling a function of one or more independent variables or predictors in the presence of an error term.

Regression Spline: A spline that is fit to data using a set of spline basis functions, typically fit using least squares.

Regression Tree: A decision tree produced in roughly two steps:

1. Divide the predictor space, $x_{1},\ x_{2},\ ...,\ x_{p}$ into $J$ distinct and non-overlapping regions, $R_{1},\ R_{2},\ ...,\ R_{J} .$
2. For every observation that falls into the region $R_{j} ,$ make the same prediction, which is the mean value of the response values for the training observations in $R_{j} .$

To determine the appropriate regions, $R_{1},\ R_{2},\ ...,\ R_{J} ,$ it is preferable to divide the predictor space into high-dimensional rectangles, or boxes, for simplicity and ease of interpretation. Ideally the goal would be to find regions that minimize the residual sum of squares given by

where $\hat{y}_{R_{j}}$ is the mean response for the training observations in the jth box. That said, it is computationally infeasible to consider every possible partition of the feature space into $J$ boxes. For this reason, a top-down, greedy approach known as recursive binary splitting is used.

Resampling Methods: Processes of repeatedly drawing samples from a data set and refitting a given model on each sample with the goal of learning more about the fitted model.

Resampling methods can be expensive since they require repeatedly performing the same statistical methods on $N$ different subsets of the data.

Residual: A quantity left over at the end of a process, a remainder or excess.

Residual Plot: A graphical tool useful for identifying non-linearity. For simple linear regression this consists of graphing the residuals, $e_{i} = y_{i} - \hat{y}_{i}$ versus the predicted or fitted values of $\hat{y}_{i} .$

If a residual plot indicates non-linearity in the model, then a simple approach is to use non-linear transformations of the predictors, such as $\log{x}$, $\sqrt{x}$, or $x^{2}$, in the regression model.

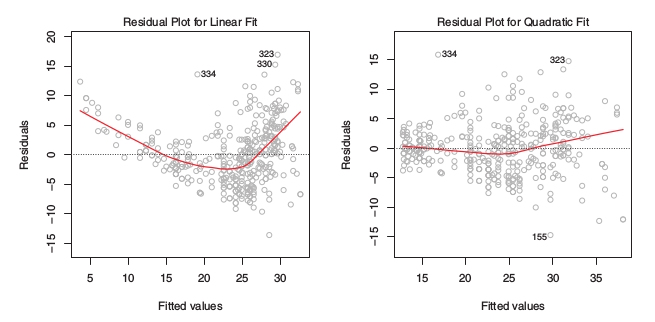
The example residual plots above suggest that a quadratic fit may be more appropriate for the model under scrutiny.

Residual Standard Error: An estimate of standard error derived from the residual sum of squares, calculated with the following formula

which simplifies to the following for simple linear regression

where $\mathrm{RSS}$ is the residual sum of squares. Expanding $\mathrm{RSS}$ yields the formula

In rough terms, the residual standard error is the average amount by which the response will deviate from the true regression line. This means that the residual standard error amounts to an estimate of the standard deviation of $\epsilon$, the irreducible error. The residual standard error can also be viewed as a measure of the lack of fit of the model to the data.

Residual Sum of Squares: The sum of the residual square differences between the $i \text{th}$ observed value and the $i \text{th}$ predicted value.

Assuming the $i \text{th}$ prediction of $Y$ is described as

then the $i \text{th}$ residual can be represented as

The residual sum of squares can then be described as

or

Ridge Regression: A shrinkage method very similar to least squares fitting except the coefficients are estimated by minimizing a modified quantity.

Recall that the least squares fitting procedure estimates the coefficients by minimizing the residual sum of squares where the residual sum of squares is given by

Ridge regression instead selects coefficients by selecting coefficients that minimize

where $\lambda$ is a tuning parameter.

The second term, $\lambda\sum_{j=1}^{p}\beta_{j}^{2} ,$ is a shrinkage penalty. In this case, the penalty is small when the coefficients are close to zero, but dependent on $\lambda$ and how the coefficients grow. As the second term grows, it pushes the coefficient estimates closer to zero, thereby shrinking them.

The tuning parameter serves to control the balance of how the two terms affect coefficient estimates. When $\lambda$ is zero, the second term is nullified, yielding estimates exactly matching those of least squares. As $\lambda$ approaches infinity, the impact of the shrinkage penalty grows, pushing/shrinking the ridge regression coefficients closer and closer to zero.

Depending on the value of $\lambda ,$ ridge regression will produce different sets of estimates, notated by $\hat{\beta}^{R}_{\lambda} ,$ for each value of $\lambda .$

It’s worth noting that the ridge regression penalty is only applied to variable coefficients, $\beta_{1}, \beta_{2}, ..., \beta_{p} ,$ not the intercept coefficient $\beta_{0} .$ Recall that the goal is to shrink the impact of each variable on the response and as such, this shrinkage should not be applied to the intercept coefficient which is a measure of the mean value of the response when none of the variables are present.

An important difference between ridge regression and least squares regression is that least squares regression’s coefficient estimates are scale equivalent and ridge regression’s are not. Because of this, it is best to apply ridge regression after standardizing the predictors.

Compared to subset methods, ridge regression is at a disadvantage when it comes to number of predictors used since ridge regression will always use all $p$ predictors. Ridge regression will shrink predictor coefficients toward zero, but it will never set any of them to exactly zero (except when $\lambda = \infty$ ). Though the extra predictors may not hurt prediction accuracy, they can make interpretability more difficult, especially when $p$ is large.

Ridge regression will tend to perform better when the response is a function of many predictors, all with coefficients roughly equal in size.

ROC Curve: A useful graphic for displaying specificity and sensitivity error rates for all possible posterior probability thresholds. ROC is a historic acronym that comes from communications theory and stands for receiver operating characteristics.

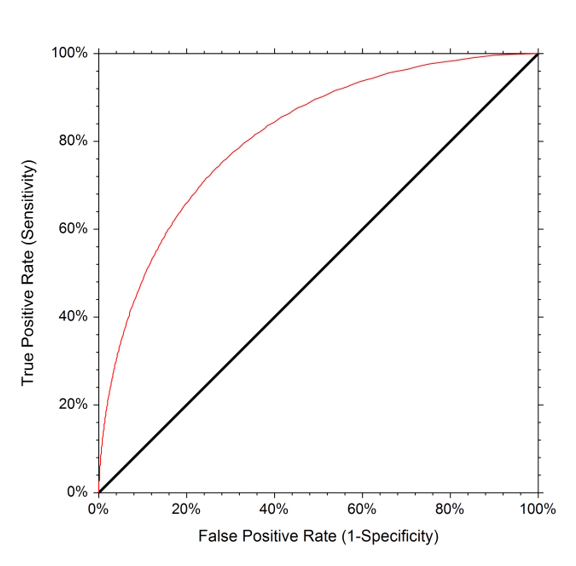
The overall performance of a classifier summarized over all possible thresholds is quantified by the area under the ROC curve.

A more ideal ROC curve will hold more tightly to the top left corner which, in turn, will increase the area under the ROC curve. A classifier that performs no better than chance will have an area under the ROC curve less than or equal to 0.5 when evaluated against a test data set.

Scale Equivalent: Typically refers to the relationship between coefficient estimates and predictor values, a system is said to be scale equivalent if the relationship between the coefficient estimates and the predictors is such that multiplying the predictors by a scalar results in a scaling of the coefficient estimates by the reciprocal of the scalar.

For example, when calculating least squares coefficient estimates, multiplying $X$ by a constant, $C ,$ leads to a scaling of the least squares coefficient estimates by a factor of $\frac{1}{C} .$ Another way of looking at it is that regardless of how the jth predictor is scaled, the value of $X_{j}\beta_{j}$ remains the same. In contrast, ridge regression coefficients can change dramatically when the scale of a given predictor is changed. This means that $X_{j}\hat{\beta}_{\lambda}^{R}$ may depend on the scaling of other predictors. Because of this, it is best to apply ridge regression after standardizing the predictors.

Shrinkage Methods: An alternative strategy to subset selection that uses all the predictors, but employs a technique to constrain or regularize the coefficient estimates.

Constraining coefficient estimates can significantly reduce their variance. Two well known techniques of shrinking regression coefficients toward zero are ridge regression and the lasso.

Shrinkage Penalty: A penalty used in shrinkage methods to shrink the impact of each variable on the response.

Sensitivity: The percentage of observations correctly positively classified (true positives).

Simple Linear Regression: A model that predicts a quantitative response $Y$ on the basis of a single predictor variable $X .$ It assumes an approximately linear relationship between $X$ and $Y .$ Formally,

where $\beta_{0}$ represents the intercept or the value of $Y$ when $X$ is equal to $0$ and $\beta_{1}$ represents the slope of the line or the average amount of change in $Y$ for each one-unit increase in $X .$

Slope: In a linear model, the average amount of change in the dependent variable, $Y ,$ for each one-unit increase in the dependent variable, $X .$

Smoothing Spline: An approach to producing a spline that utilizes a loss or penalty function to minimize the residual sum of squares while also ensuring the resulting spline is smooth. Commonly this results in a function that minimizes

where the term

is a loss function that encourages $g$ to be smooth and less variable and $\lambda$ is a non-negative tuning parameter.

Specificity: The percentage of observations correctly negatively classified (true negatives).

Standard Error: Roughly, describes the average amount that an estimate, $\hat{\mu} ,$ differs from the actual value of $\mu .$

Standard error can be useful for estimating the accuracy of a single estimated value, such as an average. To calculate the standard error of an estimated value $\hat{\mu}$, the following equation can be used:

where $\sigma$ is the standard deviation of each the observed values.

The more observations, the larger $n$, the smaller the standard error.

Standardized Values: A standardized value is the result of scaling a data point with regard to the population. More concretely, standardized values allow for putting multiple predictors on the same scale by normalizing each predictor relative to its estimated standard deviation. As a result, all the predictors will have a standard deviation of $1 .$ A formula for standardizing predictors is given by:

Step Function: A method of modeling non-linearity that splits the range of $X$ into bins and fits a different constant to each bin. This is equivalent to converting a continuous variable into an ordered categorical variable.

First, $K$ cut points, $c_{1}, c_{2}, ..., c_{k} ,$ are created in the range of $X$ from which $K + 1$ new variables are created.

where $I$ is an indicator function that returns 1 if the condition is true.

It is worth noting that each bin is unique and

since each variable only ends up in one of $K + 1$ intervals.

Once the slices have been selected, a linear model is fit using $C_{0}(X), C_{1}(X), ..., C_{K}(X)$ as predictors:

Only one of $C_{1}, C_{2}, ..., C_{K}$ can be non-zero. When $X < C ,$ all the predictors will be zero. This means $\beta_{0}$ can be interpreted as the mean value of $Y$ for $X < C_{1} .$ Similarly, for $C_{j} \leq X < C_{j+1} ,$ the linear model reduces to $\beta_{0} + \beta_{j} ,$ so $\beta_{j}$ represents the average increase in the response for $X$ in $C_{j} \leq X < C_{j+1}$ compared to $X < C_{1} .$

Unless there are natural breakpoints in the predictors, piecewise constant functions can miss the interesting data.

Studentized Residual: Because the standard deviation of residuals in a sample can vary greatly from one data point to another even when the errors all have the same standard deviation, it often does not make sense to compare residuals at different data points without first studentizing. Studentized residuals are computed by dividing each residual, $e_{i}$, by its estimated standard error. Observations whose studentized residual is greater than $|3|$ are possible outliers.

Supervised Learning: The process of inferring or modeling a function from a set of training observations where each observation consists of one or more features or predictors paired with a response measurement and the response measurement is used to guide the process of generating a model that relates the predictors to the response with the goal of accurately predicting future observations or of better inferring the relationship between the predictors and the response.

Support Vector Classifier: A classifier based on a modified version of a maximal margin classifier that does not require a separating hyperplane. Instead, a soft margin is used that almost separates the classes.

In general, a perfectly separating hyperplane can be undesirable because it can be very sensitive to individual observations. This sensitivity can also be an indication of overfitting.

A classifier based on a hyperplane that doesn’t perfectly separate the two classes can offer greater robustness to variations in individual observations and better classification of most training observations at the cost of misclassifying a few training observations.

The support vector classifier, sometimes called a soft margin classifier, allows some observations to fall on both the wrong side of the margin and the wrong side of the hyperplane.

This flexibility allows the support vector classifier to utilize a hyperplane that solves the optimization problem of maximizing $M_{\beta_{0},\ \beta_{1},\ \dots,\ \beta_{p}}$ subject to

and

where $\epsilon_{i} \geq 0$ and $\sum_{i=1}^{n}\epsilon_{i} \leq C$ where $C$ is a non-negative tuning parameter.

Like the maximal margin classifier, $M$ is the width of the margin and the focus of the optimization. $\epsilon_{1},\ \dots,\ \epsilon_{M}$ are slack variables that allow individual variables to fall on the wrong side of the margin and/or hyperplane. As with the maximal margin classifier, once an optimal solution has been found, a test observation can be classified based on the sign of

Support Vector Machine: A generalization of a simple and intuitive classifier called the maximal margin classifier. Support vector machines improve upon maximal margin classifiers by utilizing a support vector classifier which overcomes a limitation of the maximal margin classifier which requires that classes must be separable by a linear boundary. The use of the support vector classifier allows support vector machines to be applied to a wider range of cases than the maximal margin classifier. Support vector machines extend the support vector classifier to by enlarging the feature space using kernels to accommodate a non-linear boundary between classes.

When the support vector classifier is combined with a non-linear kernel, the resulting classifier is known as a support vector machine. The non-linear function underlying the support vector machine has the form

Support vector machines are intended for the binary classification setting in which there are two classes, but can be extended to handle more than two classes.

T-Distribution: Any member of the family of continuous probability distributions that arise when estimating the mean of a normally distributed population in situations where the sample size is small and population standard deviation is unknown.

T-Statistic: A measure of the number of standard deviations a quantity a quantity is from zero.

Terminal Node: Any node in a tree-like structure, such as a decision tree, that does not have any children nodes. Also known as leaf nodes or outer nodes.

Test Mean Squared Error: The mean squared error yielded when comparing a model’s predictions to the observed values from a previously unseen data set that was not used to train the model.

Total Sum of Squares: A measure of the total variance in the response $Y .$ The total sum of squares can be thought of as the total variability in the response before applying linear regression. The total sum of squares can be calculated as

Training Error Rate: The proportion of classification errors that are made when applying $\hat{f}$ to the training observations. Formally stated as,

where $\mathrm{I}$ is an indicator variable that equals $0$ when $y = \hat{y}$ and equals $1$ when $y \neq \hat{y} .$

In simple terms, the training error rate is the ratio of incorrect classifications to the count of training observations.

Training Mean Squared Error: The mean squared error yielded when comparing a model’s predictions to the observed values that were used to train that same model.

Unbiased Estimator: A model that does not systematically overestimate or underestimate when generating predictions of the true response value.

Unsupervised Learning: The process of inferring or modeling a function from a set of training observations where each observation consists of one or more features or predictors. Unlike supervised learning, no response measurement is available to supervise the analysis that goes into generating the model.

Validation Set: A randomly selected subset of a data set that is withheld for the purpose of validating model fit and estimating test error rate.

Though conceptually simple and easy to implement, the validation set approach has two potential drawbacks.

1. The estimated test error rate can be highly variable depending on which observations fall into the training set and which observations fall into the test/validation set.

2. The estimated error rate tends to be overestimated since the given statistical method was trained with fewer observations than it would have if fewer observations had been set aside for validation.

Cross-validation is a refinement of the validation set approach that mitigates these two issues.

Variable Selection: The process of removing extraneous predictors that don’t relate to the response.

Variance: The amount by which $\hat{f}$ would change or vary if it were estimated using a different training data set. In general, more flexible methods have higher variance.

Variance Inflation Factor: The ratio of the variance of $\hat{\beta}_{j}$ when fitting the full model divided by the variance of $\hat{\beta}_{j}$ if fit on its own. The smallest possible variance inflation factor value is $1.0$, which indicates no collinearity whatsoever. In practice, there is typically a small amount of collinearity among predictors. As a general rule of thumb, variance inflation factor values that exceed 5 or 10 indicate a problematic amount of collinearity.

The variance inflation factor for each variable can be computed using the formula

where $\mathrm{R}_{x_{j}|x_{-j}}$ is the $\mathrm{R}^{2}$ from a regression of $X_{j}$ onto all of the other predictors. If $\mathrm{R}_{x_{j}|x_{-j}}$ is close to one, the VIF will be large and collinearity is present.

Z-Statistic: Similar to the t-statistic, logistic regression measures the accuracy of coefficient estimates using a quantity called the z-statistic. The z-statistic for $\beta_{1}$ is represented by

A large z-statistic offers evidence against the null hypothesis.