stats-learning-notes

Previous: Chapter 2 - Statistical Learning

Chapter 3 - Linear Regression

Simple Linear Regression

Simple linear regression predicts a quantitative response $Y$ on the basis of a single predictor variable $X .$ It assumes an approximately linear relationship between $X$ and $Y .$ Formally,

$\normalsize Y \approx \beta_{0} + \beta_{1}X$

where $\beta_{0}$ represents the intercept or the value of $Y$ when $X$ is equal to $0$ and $\beta_{1}$ represents the slope of the line or the average amount of change in $Y$ for each one-unit increase in $X .$

Together, $\beta_{0}$ and $\beta_{1}$ are known as the model coefficients or parameters.

Estimating Model Coefficients

Since $\beta_{0}$ and $\beta_{1}$ are typically unknown, it is first necessary to estimate the coefficients before making predictions. To estimate the coefficients, it is desirable to choose values for $\beta_{0}$ and $\beta_{1}$ such that the resulting line is as close as possible to the observed data points.

There are many ways of measuring closeness. The most common method strives to minimizes the sum of the residual square differences between the $i \text{th}$ observed value and the $i \text{th}$ predicted value.

Assuming the $i \text{th}$ prediction of $Y$ is described as

$\normalsize \hat{y_{i}} = \hat{\beta_{0}} + \hat{\beta_{1}}x_{i}$

then the $i \text{th}$ residual can be represented as

$\normalsize e_{i} = y_{i} - \hat{y_{i}} = y_{i} - \hat{\beta_{0}} - \hat{\beta_{1}}x_{i} .$

The residual sum of squares can then be described as

$\normalsize RSS = e_{1}^2 + e_{2}^2 + \ldots + e_{n}^2$

$\normalsize RSS = (y_{1} - \hat{\beta_{0}} - \hat{\beta_{1}}x_{1})^2 + (y_{2} - \hat{\beta_{0}} - \hat{\beta_{1}}x_{2})^2 + \ldots + (y_{n} - \hat{\beta_{0}} - \hat{\beta_{1}}x_{n})^2 .$

Assuming sample means of

$\normalsize \bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_{i}$

and

$\normalsize \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_{i} ,$

calculus can be applied to estimate the least squares coefficient estimates for linear regression to minimize the residual sum of squares like so

$\normalsize \beta_{1} = \frac{\sum_{i=1}^{n}(x_{i} - \bar{x})(y_{i} - \bar{y})}{\sum_{i=1}^{n}(x_{i} - \bar{x})^2}$ $\normalsize \beta_{0} = \bar{y} - \hat{\beta_{1}}\bar{x}$

Assessing Coefficient Estimate Accuracy

Simple linear regression represents the relationship between $Y$ and $X$ as

$\normalsize Y = \beta_{0} + \beta_{1}X + \epsilon$

where $\beta_{0}$ is the intercept term, or the value of $Y$ when $X = 0$ ; $\beta_{1}$ is the slope, or average increase in $Y$ associated with a one-unit increase in $X$ ; and $\epsilon$ is the error term which acts as a catchall for what is missed by the simple model given that the true relationship likely isn’t linear, there may be other variables that affect $Y$ , and/or there may be error in the observed measurements. The error term is typically assumed to be independent of $X .$

The model used by simple linear regression defines the population regression line, which describes the best linear approximation to the true relationship between $X$ and $Y$ for the population.

The coefficient estimates yielded by least squares regression characterize the least squares line,

$\normalsize \hat{y_{i}} = \hat{\beta_{0}} + \hat{\beta_{1}}x_{i} .$

The difference between the population regression line and the least squares line is similar to the difference that emerges when using a sample to estimate the characteristics of a large population.

In linear regression, the unknown coefficients, $\beta_{0}$ and $\beta_{1}$ define the population regression line, whereas the estimates of those coefficients, $\hat{\beta_{0}}$ and $\hat{\beta_{1}}$ define the least squares line.

Though the parameter estimates for a given sample may overestimate or underestimate the value of a particular parameter, an unbiased estimator does not systemically overestimate or underestimate the true parameter.

This means that using an unbiased estimator and a large number of data sets, the values of the coefficients $\beta_{0}$ and $\beta_{1}$ could be determined by averaging the coefficient estimates from each of those data sets.

To estimate the accuracy of a single estimated value, such as an average, it can be helpful to calculate the standard error of the estimated value $\hat{\mu}$ , which can be accomplished like so

$\normalsize \mathrm{Var}(\hat{\mu}) = \mathrm{SE}(\hat{\mu})^2 = \frac{\sigma^{2}}{n}$

where $\sigma$ is the standard deviation of each $y_{i} .$

Roughly, the standard error describes the average amount that the estimate $\hat{\mu}$ differs from $\mu .$

The more observations, the larger $n$ , the smaller the standard error.

To compute the standard errors associated with $\beta_{0}$ and $\beta_{1}$ , the following formulas can be used:

$\normalsize \mathrm{SE}(\beta_{0})^{2} = \sigma^{2}\bigg[\frac{1}{n} + \frac{\bar{x}^{2}}{\sum_{i=1}^{n}(x_{i} - \bar{x})^2}\bigg]$

and

$\normalsize \mathrm{SE}(\beta_{1})^{2} = \frac{\sigma^{2}}{\sum_{i=1}^{n}(x_{i} - \bar{x})^2}$

where $\sigma^{2} = \mathrm{Var}(\epsilon)$ and $\epsilon_{i}$ is not correlated with $\sigma^{2} .$

$\sigma^{2}$ generally isn’t known, but can be estimated from the data. The estimate of $\sigma$ is known as the residual standard error and can be calculated with the following formula

$\normalsize \mathrm{RSE} = \sqrt{\frac{\mathrm{RSS}}{(n - 2)}}$

where $\mathrm{RSS}$ is the residual sum of squares.

Standard errors can be used to compute confidence intervals and prediction intervals.

A confidence interval is defined as a range of values such that there’s a certain likelihood that the range will contain the true unknown value of the parameter.

For simple linear regression the 95% confidence interval for $\beta_{1}$ can be approximated by

$\normalsize \hat{\beta_{1}} \pm 2 \times \mathrm{SE}(\hat{\beta_{1}}) .$

Similarly, a confidence interval for $\beta_{0}$ can be approximated as

$\normalsize \hat{\beta_{0}} \pm 2 \times \mathrm{SE}(\hat{\beta_{0}}) .$

The accuracy of an estimated prediction depends on whether we wish to predict an individual response, $y = f(x) + \epsilon$ , or the average response, $f(x) .$

When predicting an individual response, $y = f(x) + \epsilon$ , a prediction interval is used.

When predicting an average response, $f(x)$ , a confidence interval is used.

Prediction intervals will always be wider than confidence intervals because they take into account the uncertainty associated with $\epsilon$ , the irreducible error.

The standard error can also be used to perform hypothesis testing on the estimated coefficients.

The most common hypothesis test involves testing the null hypothesis that states

$H_{0}$ : There is no relationship between $X$ and $Y$

versus the alternative hypothesis

$H_{1}$ : Thee is some relationship between $X$ and $Y .$

In mathematical terms, the null hypothesis corresponds to testing if $\beta_{1} = 0$ , which reduces to

$\normalsize Y = \beta_{0} + \epsilon$

which evidences that $X$ is not related to $Y .$

To test the null hypothesis, it is necessary to determine whether the estimate of $\beta_{1}$ , $\hat{\beta_{1}}$ , is sufficiently far from zero to provide confidence that $\beta_{1}$ is non-zero.

How close is close enough depends on $\mathrm{SE}(\hat{\beta_{1}}) .$ When $\mathrm{SE}(\hat{\beta_{1}})$ is small, then small values of $\hat{\beta_{1}}$ may provide strong evidence that $\beta_{1}$ is not zero. Conversely, if $\mathrm{SE}(\hat{\beta_{1}})$ is large, then $\hat{\beta_{1}}$ will need to be large in order to reject the null hypothesis.

In practice, computing a T-statistic, which measures the number of standard deviations that $\hat{\beta_{1}}$ , is away from $0$ , is useful for determining if an estimate is sufficiently significant to reject the null hypothesis.

A T-statistic can be computed as follows

$\normalsize t = \frac{\hat{\beta}_{1} - 0}{\mathrm{SE}(\hat{\beta_{1}})}$

If there is no relationship between $X$ and $Y$ , it is expected that a t-distribution with $n - 2$ degrees of freedom should be yielded.

With such a distribution, it is possible to calculate the probability of observing a value of $|t|$ or larger assuming that $\hat{\beta_{1}} = 0 .$ This probability, called the p-value, can indicate an association between the predictor and the response if sufficiently small.

Assessing Model Accuracy

Once the null hypothesis has been rejected, it may be desirable to quantify to what extent the model fits the data. The quality of a linear regression model is typically assessed using residual standard error (RSE) and the $R^{2}$ statistic statistic.

The residual standard error is an estimate of the standard deviation of $\epsilon$ , the irreducible error.

In rough terms, the residual standard error is the average amount by which the response will deviate from the true regression line.

For linear regression, the residual standard error can be computed as

$\normalsize \mathrm{RSE} = \sqrt{\frac{1}{n-2}\mathrm{RSS}} = \sqrt{\frac{1}{n-2}\sum_{i=1}^{n}(y_{i} - \hat{y}_{i})^{2}}$

The residual standard error is a measure of the lack of fit of the model to the data. When the values of $y_{i} \approx \hat{y}_{i}$ , the RSE will be small and the model will fit the data well. Conversely, if $y_{i} \ne \hat{y_{i}}$ for some values, the RSE may be large, indicating that the model doesn’t fit the data well.

The RSE provides an absolute measure of the lack of fit of the model in the units of $Y .$ This can make it difficult to know what constitutes a good RSE value.

The $R^{2}$ statistic is an alternative measure of fit that takes the form of a proportion. The $R^{2}$ statistic captures the proportion of variance explained as a value between $0$ and $1$ , independent of the unit of $Y .$

To calculate the $R^2$ statistic, the following formula may be used

$\normalsize R^{2} = \frac{\mathrm{TSS}-\mathrm{RSS}}{\mathrm{TSS}} = 1 - \frac{\mathrm{RSS}}{\mathrm{TSS}}$

where

$\normalsize \mathrm{RSS} = \sum_{i=1}^{n}(y_{i} - \hat{y}_{i})^{2}$

and

$\normalsize \mathrm{TSS} = \sum_{i=1}^{n}(y_{i} - \bar{y}_{i})^{2} .$

The total sum of squares, TSS, measures the total variance in the response $Y .$ The TSS can be thought of as the total variability in the response before applying linear regression. Conversely, the residual sum of squares, RSS, measures the amount of variability left after performing the regression.

Ergo, $TSS - RSS$ measures the amount of variability in the response that is explained by the model. $R^{2}$ measures the proportion of variability in $Y$ that can be explained by $X .$ An $R^{2}$ statistic close to $1$ indicates that a large portion of the variability in the response is explained by the model. An $R^{2}$ value near $0$ indicates that the model accounted for very little of the variability of the model.

An $R^{2}$ value near $0$ may occur because the linear model is wrong and/or because the inherent $\sigma^{2}$ is high.

$R^{2}$ has an advantage over RSE since it will always yield a value between $0$ and $1$ , but it can still be tough to know what a good $R^{2}$ value is. Frequently, what constitutes a good $R^{2}$ value depends on the application and what is known about the problem.

The $R^{2}$ statistic is a measure of the linear relationship between $X$ and $Y .$

Correlation is another measure of the linear relationship between $X$ and $Y .$ Correlation of can be calculated as

$\normalsize \mathrm{Cor}(X,Y) = \frac{\sum_{i=1}^{n}(x_{i} - \bar{x})(y_{i} - \bar{y})}{\sqrt{\sum_{i=1}^{n}(x_{i} - \bar{x})^{2}}\sqrt{\sum_{i=1}^{n}(y_{i}-\bar{y})^{2}}}$

This suggests that $r = \mathrm{Cor}(X,Y)$ could be used instead of $R^{2}$ to assess the fit of the linear model, however for simple linear regression it can be shown that $R^{2} = r^{2} .$ More concisely, for simple linear regression, the squared correlation and the $R^{2}$ statistic are equivalent. Though this is the case for simple linear regression, correlation does not extend to multiple linear regression since correlation quantifies the association between a single pair of variables. The $R^{2}$ statistic can, however, be applied to multiple regression.

Multiple Regression

The multiple linear regression model takes the form of

$\normalsize Y = \beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2} + \ldots + \beta_{p}X_{p} + \epsilon .$

Multiple linear regression extends simple linear regression to accommodate multiple predictors.

$X_{j}$ represents the $j \text{th}$ predictor and $\beta_{j}$ represents the average effect of a one-unit increase in $X_{j}$ on $Y$ , holding all other predictors fixed.

Estimating Multiple Regression Coefficients

Because the coefficients $\beta_{0}, \beta_{1}, \ldots, \beta_{p}$ are unknown, it is necessary to estimate their values. Given estimates of $\hat{\beta_{0}}, \hat{\beta_{1}}, \ldots, \hat{\beta_{p}}$ , estimates can be made using the formula below

$\normalsize \hat{y} = \hat{\beta_{0}} + \hat{\beta_{1}}x_{1} + \hat{\beta_{2}}x_{2} + \ldots + \hat{\beta_{p}}x_{p}$

The parameters $\hat{\beta_{0}}, \hat{\beta_{1}}, \ldots, \hat{\beta_{p}}$ can be estimated using the same least squares strategy as was employed for simple linear regression. Values are chosen for the parameters $\hat{\beta_{0}}, \hat{\beta_{1}}, \ldots, \hat{\beta_{p}}$ such that the residual sum of squares is minimized

$\normalsize RSS = \sum_{i=1}^{n}(y_{i} - \hat{y}_{i})^{2} = \sum_{i=1}^{n}(y_{i} - \hat{\beta_{0}} - \hat{\beta_{1}}x_{1} - \hat{\beta_{2}}x_{2} - \ldots - \hat{\beta_{p}}x_{p})^{2}$

Estimating the values of these parameters is best achieved with matrix algebra.

Assessing Multiple Regression Coefficient Accuracy

Once estimates have been derived, it is next appropriate to test the null hypothesis

$\normalsize H_{0}: \beta_{1} = \beta_{2} = \ldots = \beta_{p} = 0$

versus the alternative hypothesis

$H_{a}: at\ least\ one\ of B_{j} \ne 0 .$

The F-statistic can be used to determine which hypothesis holds true.

The F-statistic can be computed as

$\normalsize \mathrm{F} = \frac{(\mathrm{TSS} - \mathrm{RSS})/p}{\mathrm{RSS}/(n - p - 1)} = \frac{\frac{\mathrm{TSS} - \mathrm{RSS}}{p}}{\frac{\mathrm{RSS}}{n - p - 1}}$

where, again,

$\normalsize \mathrm{TSS} = \sum_{i=1}^{n}(y_{i} - \bar{y}_{i})^{2}$

and

$\normalsize \mathrm{RSS} = \sum_{i=1}^{n}(y_{i} - \hat{y}_{i})^2$

If the assumptions of the linear model, represented by the alternative hypothesis, are true it can be shown that

$\normalsize \mathrm{E}\{\frac{\mathrm{RSS}}{n - p - 1}\} = \sigma^{2}$

Conversely, if the null hypothesis is true, it can be shown that

$\normalsize \mathrm{E}\{\frac{\mathrm{TSS} - \mathrm{RSS}}{p}\} = \sigma^{2}$

This means that when there is no relationship between the response and the predictors the F-statisitic takes on a value close to $1 .$

Conversely, if the alternative hypothesis is true, then the F-statistic will take on a value greater than $1 .$

When $n$ is large, an F-statistic only slightly greater than $1$ may provide evidence against the null hypothesis. If $n$ is small, a large F-statistic is needed to reject the null hypothesis.

When the null hypothesis is true and the errors $\epsilon_{i}$ have a normal distribution, the F-statistic follows and F-distribution. Using the F-distribution, it is possible to figure out a p-value for the given $n$ , $p$ , and F-statistic. Based on the obtained p-value, the validity of the null hypothesis can be determined.

It is sometimes desirable to test that a particular subset of $q$ coefficients are $0 .$ This equates to a null hypothesis of

$\normalsize H_{0}: \beta_{p - q + 1} = \beta_{p - q + 2} = \ldots = \beta_{p} = 0 .$

Supposing that the residual sum of squares for such a model is $\mathrm{RSS}_{0}$ then the F-statistic could be calculated as

$\normalsize \mathrm{F} = \frac{(\mathrm{RSS}_{0} - \mathrm{RSS})/q}{\mathrm{RSS}/(n - p - 1)} = \frac{\frac{\mathrm{RSS}_{0} - \mathrm{RSS}}{q}}{\frac{\mathrm{RSS}}{n - p - 1}} .$

Even in the presence of p-values for each individual variable, it is still important to consider the overall F-statistic because there is a reasonably high likelihood that a variable with a small p-value will occur just by chance, even in the absence of any true association between the predictors and the response.

In contrast, the F-statistic does not suffer from this problem because it adjusts for the number of predictors. The F-statistic is not infallible and when the null hypothesis is true the F-statistic can still result in p-values below $0.05$ about 5% of the time regardless of the number of predictors or the number of observations.

The F-statistic works best when $p$ is relatively small or when $p$ is relatively small compared to $n .$

When $p$ is greater than $n$ , multiple linear regression using least squares will not work, and similarly, the F-statistic cannot be used either.

Selecting Important Variables

Once it has been established that at least one of the predictors is associated with the response, the question remains, which of the predictors is related to the response? The process of removing extraneous predictors that don’t relate to the response is called variable selection.

Ideally, the process of variable selection would involve testing many different models, each with a different subset of the predictors, then selecting the best model of the bunch, with the meaning of “best” being derived from various statistical methods.

Regrettably, there are a total of $2^{p}$ models that contain subsets of $p$ predictors. Because of this, an efficient and automated means of choosing a smaller subset of models is needed. There are a number of statistical approaches to limiting the range of possible models.

Forward selection begins with a null model, a model that has an intercept but no predictors, and attempts $p$ simple linear regressions, keeping whichever predictor results in the lowest residual sum of squares. In this fashion, the predictor yielding the lowest RSS is added to the model one-by-one until some halting condition is met. Forward selection is a greedy process and it may include extraneous variables.

Backward selection begins with a model that includes all the predictors and proceeds by removing the variable with the highest p-value each iteration until some stopping condition is met. Backwards selection cannot be used when $p > n .$

Mixed selection begins with a null model, like forward selection, repeatedly adding whichever predictor yields the best fit. As more predictors are added, the p-values become larger. When this happens, if the p-value for one of the variables exceeds a certain threshold, that variable is removed from the model. The selection process continues in this forward and backward manner until all the variables in the model have sufficiently low p-values and all the predictors excluded from the model would result in a high p-value if added to the model.

Assessing Multiple Regression Model Fit

While in simple linear regression the $\mathrm{R}^{2}$ , the fraction of variance explained, is equal to $\mathrm{Cor}(X, Y) ,$ in multiple linear regression, $\mathrm{R}^{2}$ is equal to $\mathrm{Cor}(Y, \hat{Y})^{2} .$ In other words, $\mathrm{R}^{2}$ is equal to the square of the correlation between the response and the fitted linear model. In fact, the fitted linear model maximizes this correlation among all possible linear models.

An $\mathrm{R}^{2}$ close to $1$ indicates that the model explains a large portion of the variance in the response variable. However, it should be noted that $\mathrm{R}^{2}$ will always increase when more variables are added to the model, even when those variables are only weakly related to the response. This happens because adding another variable to the least squares equation will always yield a closer fit to the training data, though it won’t necessarily yield a closer fit to the test data.

Residual standard error, RSE, can also be used to assess the fit of a multiple linear regression model. In general, RSE can be calculated as

$\normalsize RSE = \sqrt{\frac{\mathrm{RSS}}{n - p - 1}}$

which simplifies to the following for simple linear regression

$\normalsize RSE = \sqrt{\frac{\mathrm{RSS}}{n - 2}} .$

Given the definition of RSE for multiple linear regression, it can be seen that models with more variables can have a higher RSE if the decrease in RSS is small relative to the increase in $p .$

In addition to $\mathrm{R}^{2}$ and RSE, it can also be useful to plot the data to verify the model.

Once coefficients have been estimated, making predictions is a simple as plugging the coefficients and predictor values into the multiple linear model

$\normalsize \hat{y} = \hat{\beta_{0}} + \hat{\beta_{1}}x_{1} + \hat{\beta_{2}}x_{2} + \ldots + \hat{\beta_{p}}x_{p} .$

However, it should be noted that these predictions will be subject to three types of uncertainty.

The coefficient estimates, $\hat{\beta}_{0}, \hat{\beta}_{1}, \ldots, \hat{\beta}_{p},$ are only estimates of the actual coefficients $\beta_{0}, \beta_{1}, \ldots, \beta_{p}.$ That is to say, the least squares plane is only an estimate of the true population regression plane. The error introduced by this inaccuracy is reducible error and a confidence interval can be computed to determine how close $\hat{y}$ is to $f(X) .$
Assuming a linear model for $f(X)$ is almost always an approximation of reality, which means additional reducible error is introduced due to model bias. A linear model often models the best linear approximation of the true, non-linear surface.
Even in the case where $f(X)$ and the true values of the coefficients, $\beta_{0}, \ldots,, \beta_{p}$ are known, the response value cannot be predicted exactly because of the random, irreducible error $\epsilon$ , in the model. How much $\hat{Y}$ will tend to vary from $Y$ can be determined using prediction intervals.

Prediction intervals will always be wider than confidence intervals because they incorporate both the error in the estimate of $f(X)$ , the reducible error, and the variation in how each point differs from the population regression plane, the irreducible error.

Qualitative predictors

Linear regression can also accommodate qualitative variables.

When a qualitative predictor or factor has only two possible values or levels, it can be incorporated into the model my introducing an indicator variable or dummy variable that takes on only two numerical values.

For example, using a coding like

$\normalsize X_{i} = \left\{ \begin{array}{cc} 1&\mathrm{if\ p_{i}\ =\ class\ A}\\ 0&\mathrm{if\ p_{i}\ =\ class\ B} \end{array} \right.$

yields a regression equation like

$\normalsize y_{i} = \beta_{0} + \beta_{1}X_{1} + \epsilon_{i} = \left\{ \begin{array}{cc} \beta_{0} + \beta_{1} + \epsilon_{i}&\mathrm{if\ p_{i}\ =\ class\ A}\\ \beta_{0} + \epsilon_{i}&\mathrm{if\ p_{i}\ =\ class\ B} \end{array} \right.$

Given such a coding, $\beta_{1}$ represents the average difference in $X_{1}$ between classes A and B.

Alternatively, a dummy variable like the following could be used

$\normalsize X_{i} = \left\{ \begin{array}{cc} 1&\mathrm{if\ p_{i}\ =\ class\ A}\\ -1&\mathrm{if\ p_{i}\ =\ class\ B} \end{array} \right.$

which results in a regression model like

$\normalsize y_{i} = \beta_{0} + \beta_{1}X_{1} + \epsilon_{i} = \left\{ \begin{array}{cc} \beta_{0} + \beta_{1} + \epsilon_{i}&\mathrm{if\ p_{i}\ =\ class\ A}\\ \beta_{0} - \beta_{1} + \epsilon_{i}&\mathrm{if\ p_{i}\ =\ class\ B} \end{array} \right. .$

In which case, $\beta_{0}$ represents the overall average and $\beta_{1}$ is the amount class A is above the average and class B below the average.

Regardless of the coding scheme, the predictions will be equivalent. The only difference is the way the coefficients are interpreted.

When a qualitative predictor takes on more than two values, a single dummy variable cannot represent all possible values. Instead, multiple dummy variables can be used. The number of variables required will always be one less than the number of values that the predictor can take on.

For example, with a predictor that can take on three values, the following coding could be used

$\normalsize X_{i1} = \left\{ \begin{array}{cc} 1&\mathrm{if\ p_{i}\ =\ class\ A}\\ 0&\mathrm{if\ p_{i}\ \ne\ class\ A} \end{array} \right.$ $\normalsize X_{i2} = \left\{ \begin{array}{cc} 1&\mathrm{if\ p_{i}\ =\ class\ B}\\ 0&\mathrm{if\ p_{i}\ \ne\ class\ B} \end{array} \right.$ $\normalsize y_{i} = \beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2} + \epsilon_{i} = \left\{ \begin{array}{cc} \beta_{0} + \beta_{1} + \epsilon_{i}&\mathrm{if\ p_{i}\ =\ class\ A}\\ \beta_{0} + \beta_{2} + \epsilon_{i}&\mathrm{if\ p_{i}\ =\ class\ B}\\ \beta_{0} + \epsilon_{i}&\mathrm{if\ p_{i}\ =\ class\ C} \end{array} \right. .$

With such a coding, $\beta_{0}$ can be interpreted as the average response for class C. $\beta_{1}$ can be interpreted as the average difference in response between classes A and C. Finally, $\beta_{2}$ can be interpreted as the average difference in response between classes B and C.

The case where $\beta_{1}$ and $\beta_{2}$ are both zero, the level with no dummy variable, is known as the baseline.

Using dummy variables allows for easily mixing quantitative and qualitative predictors.

There are many ways to encode dummy variables. Each approach yields equivalent model fits, but results in different coefficients and different interpretations that highlight different contrasts.

Extending the Linear Model

Though linear regression provides interpretable results, it makes several highly restrictive assumptions that are often violated in practice. One assumption is that the relationship between the predictors and the response is additive. Another assumption is that the relationship between the predictors and the response is linear.

The additive assumption implies that the effect of changes in a predictor $X_{j}$ on the response $Y$ is independent of the values of the other predictors.

The linear assumption implies that the change in the response $Y$ due to a one-unit change in $X_{j}$ is constant regardless of the value of $X_{j} .$

The additive assumption ignores the possibility of an interaction between predictors. One way to account for an interaction effect is to include an additional predictor, called an interaction term, that computes the product of the associated predictors.

Modeling Predictor Interaction

A simple linear regression model account for interaction between the predictors would look like

$\normalsize \mathrm{Y} = \beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2} + \beta_{3}X_{1}X_{2} + \epsilon$

$\beta_{3}$ can be interpreted as the increase in effectiveness of $\beta_{1}$ given a one-unit increase in $\beta_{2}$ and vice-versa.

It is sometimes possible for an interaction term to have a very small p-value while the associated main effects, $X_{1}, X_{2}, etc.$ , do not. Even in such a scenario the main effects should still be included in the model due to the hierarchical principle.

The hierarchical principle states that, when an interaction term is included in the model, the main effects should also be included, even if the p-values associated with their coefficients are not significant. The reason for this is that $X_{1}X_{2}$ is often correlated with $X_{1}$ and $X_{2}$ and removing them tends to change the meaning of the interaction.

If $X_{1}X_{2}$ is related to the response, then whether or not the coefficient estimates of $X_{1}$ or $X_{2}$ are exactly zero is of limited interest.

Interaction terms can also model a relationship between a quantitative predictor and a qualitative predictor.

In the case of simple linear regression with a qualitative variable and without an interaction term, the model takes the form

$\normalsize y_{i} = \beta_{0} + \beta_{1}X_{1} + \left\{ \begin{array}{cc} \beta_{2}&\mathrm{if\ p_{i}\ =\ class\ A}\\ 0&\mathrm{if\ p_{i}\ \ne\ class\ A} \end{array} \right.$

with the addition of an interaction term, the model takes the form

$\normalsize y_{i} = \beta_{0} + \beta_{1}X_{1} + \left\{ \begin{array}{cc} \beta_{2} + \beta_{3}X_{1}&\mathrm{if\ p_{i}\ =\ class\ A}\\ 0&\mathrm{if\ p_{i}\ \ne\ class\ A} \end{array} \right.$

which is equivalent to

$\normalsize y_{i} = \left\{ \begin{array}{cc} (\beta_{0} + \beta_{2}) + (\beta_{1} + \beta_{3})X_{1}&\mathrm{if\ p_{i}\ =\ class\ A}\\ \beta_{0} + \beta_{1}X_{1}&\mathrm{if\ p_{i}\ \ne\ class\ A} \end{array} \right.$

Modeling Non-Linear Relationships

To mitigate the effects of the linear assumption it is possible to accommodate non-linear relationships by incorporating polynomial functions of the predictors in the regression model.

For example, in a scenario where a quadratic relationship seems likely, the following model could be used

$\normalsize Y_{i} = \beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{1}^{2} + \epsilon$

This extension of the linear model to accommodate non-linear relationships is called polynomial regression.

Common Problems with Linear Regression

Non-linearity of the response-predictor relationship
Correlation of error terms
Non-constant variance of error terms
Outliers
High-leverage points
Collinearity

1. Non-linearity of the response-predictor relationship

If the true relationship between the response and predictors is far from linear, then virtually all conclusions that can be drawn from the model are suspect and prediction accuracy can be significantly reduced.

Residual plots are a useful graphical tool for identifying non-linearity. For simple linear regression this consists of graphing the residuals, $e_{i} = y_{i} - \hat{y}_{i}$ versus the predicted or fitted values of $\hat{y}_{i} .$

If a residual plot indicates non-linearity in the model, then a simple approach is to use non-linear transformations of the predictors, such as $\log{x}$ , $\sqrt{x}$ , or $x^{2}$ , in the regression model.

Residual plot for linear and quadratic fits of same data set

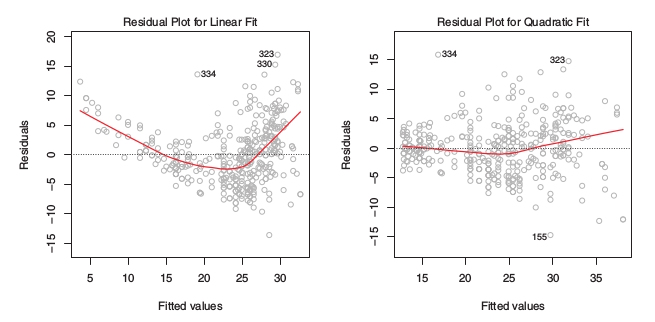
The example residual plots above suggest that a quadratic fit may be more appropriate for the model under scrutiny.

2. Correlation of error terms

An important assumption of linear regression is that the error terms, $\epsilon_{1}, \epsilon_{2}, \ldots, \epsilon_{n}$ , are uncorrelated. Because the estimated regression coefficients are calculated based on the assumption that the error terms are uncorrelated, if the error terms are correlated it will result in incorrect standard error values that will tend to underestimate the true standard error. This will result in prediction intervals and confidence intervals that are narrower than they should be. In addition, p-values associated with the model will be lower than they should be. In other words, correlated error terms can make a model appear to be stronger than it really is.

Correlations in error terms can be the result of time series data, unexpected observation relationships, and other environmental factors. Observations that are obtained at adjacent time points will often have positively correlated errors. Good experiment design is also a crucial factor in limiting correlated error terms.

3. Non-constant variance of error terms

Linear regression also assumes that the error terms have a constant variance,

$\normalsize \mathrm{Var}(\epsilon_{i}) = \sigma^{2} .$

Standard errors, confidence intervals, and hypothesis testing all depend on this assumption.

Residual plots can help identify non-constant variances in the error, or heteroscedasticity, if a funnel shape is present.

Residual plot with funnel shape due to non-constant variance of error
terms

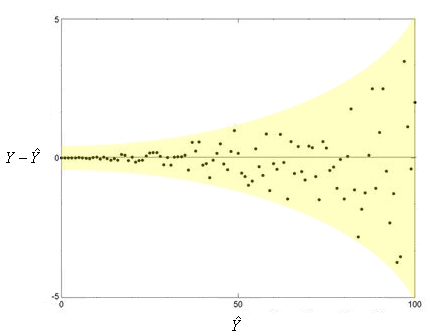
One way to address this problem is to transform the response $Y$ using a concave function such as $\log{Y}$ or $\sqrt{Y} .$ This results in a greater amount of shrinkage of the larger responses, leading to a reduction in heteroscedasticity.

4. Outliers

An outlier is a point for which $y_{i}$ is far from the value predicted by the model.

Excluding outliers can result in improved residual standard error and improved $\mathrm{R}^{2}$ values, usually with negligible impact to the least squares fit.

Residual plots can help identify outliers, though it can be difficult to know how big a residual needs to be before considering a point an outlier. To address this, it can be useful to plot the studentized residuals instead of the normal residuals. Studentized residuals are computed by dividing each residual, $e_{i}$ , by its estimated standard error. Observations whose studentized residual is greater than $|3|$ are possible outliers.

Outliers should only be removed when confident that the outliers are due to a recording or data collection error since outliers may otherwise indicate a missing predictor or other deficiency in the model.

5. High-Leverage Points

While outliers relate to observations for which the response $y_{i}$ is unusual given the predictor $x_{i}$ , in contrast, observations with high leverage are those that have an unusual value for the predictor $x_{i}$ for the given response $y_{i} .$

High leverage observations tend to have a sizable impact on the estimated regression line and as a result, removing them can yield improvements in model fit.

For simple linear regression, high leverage observations can be identified as those for which the predictor value is outside the normal range. With multiple regression, it is possible to have an observation for which each individual predictor’s values are well within the expected range, but that is unusual in terms of the combination of the full set of predictors.

To qualify an observation’s leverage, the leverage statistic can be computed.

A large leverage statistic indicates an observation with high leverage.

For simple linear regression, the leverage statistic can be computed as

$\normalsize h_{i} = \frac{1}{n} + \frac{(x_{i} - \bar{x})^{2}}{\sum_{j=1}^{n}(x_{j} - \bar{x})^{2}} .$

The leverage statistic always falls between $\frac{1}{n}$ and $1$ and the average leverage is always equal to $\frac{p + 1}{n} .$ So, if an observation has a leverage statistic greatly exceeds $\frac{p + 1}{n}$ then it may be evidence that the corresponding point has high leverage.

6. Collinearity

Collinearity refers to the situation in which two or more predictor variables are closely related to one another.

Collinearity can pose problems for linear regression because it can make it hard to determine the individual impact of collinear predictors on the response.

Collinearity reduces the accuracy of the regression coefficient estimates, which in turn causes the standard error of $\beta_{j}$ to grow. Since the T-statistic for each predictor is calculated by dividing $\beta_{j}$ by its standard error, collinearity results in a decline in the true T-statistic. This may cause it to appear that $\beta_{j}$ and $x_{j}$ are related to the response when they are not. As such, collinearity reduces the effectiveness of the null hypothesis. Because of all this, it is important to address possible collinearity problems when fitting the model.

One way to detect collinearity is to generate a correlation matrix of the predictors. Any element in the matrix with a large absolute value indicates highly correlated predictors. This is not always sufficient though, as it is possible for collinearity to exist between three or more variables even if no pair of variables have high correlation. This scenario is known as multicollinearity.

Multicollinearity can be detected by computing the variance inflation factor. The variance inflation factor is the ratio of the variance of $\hat{\beta}_{j}$ when fitting the full model divided by the variance of $\hat{\beta}_{j}$ if fit on its own. The smallest possible VIF value is $1.0$ , which indicates no collinearity whatsoever. In practice, there is typically a small amount of collinearity among predictors. As a general rule of thumb, VIF values that exceed 5 or 10 indicate a problematic amount of collinearity.

The variance inflation factor for each variable can be computed using the formula

$\normalsize \mathrm{VIF}(\hat{\beta_{j}}) = \frac{1}{1 - \mathrm{R}_{x_{j}|x_{-j}}^{2}}$

where $\mathrm{R}_{x_{j}|x_{-j}}$ is the $\mathrm{R}^{2}$ from a regression of $X_{j}$ onto all of the other predictors. If $\mathrm{R}_{x_{j}|x_{-j}}$ is close to one, the VIF will be large and collinearity is present.

One way to handle collinearity is to drop one of the problematic variables. This usually doesn’t compromise the fit of the regression as the collinearity implies that the information that the predictor provides about the response is abundant.

A second means of handling collinearity is to combine the collinear predictors together into a single predictor by some kind of transformation such as an average.

Parametric Methods Versus Non-Parametric Methods

A non-parametric method akin to linear regression is k-nearest neighbors regression which is closely related to the k-nearest neighbors classifier.

Given a value for $K$ and a prediction point $x_{0}$ , k-nearest neighbors regression first identifies the $K$ observations that are closest to $x_{0}$ , represented by $N_{0} .$ $f(x_{0})$ is then estimated using the average of $N_{0i}$ like so

$\normalsize \hat{f}(x_{0}) = \frac{1}{k}\sum_{x_{i} \in N_{0}}y_{i}$

A parametric approach will outperform a non-parametric approach if the parametric form is close to the true form of $f(X) .$

The choice of a parametric approach versus a non-parametric approach will depend largely on the bias-variance trade-off and the shape of the function $f(X) .$

When the true relationship is linear, it is difficult for a non-parametric approach to compete with linear regression because the non-parametric approach incurs a cost in variance that is not offset by a reduction in bias. Additionally, in higher dimensions, K-nearest neighbors regression often performs worse than linear regression. This is often due to combining too small an $n$ with too large a $p$ , resulting in a given observation having no nearby neighbors. This is often called the curse of dimensionality. In other words, the $K$ observations nearest to an observation may be far away from $x_{0}$ in a $p$ -dimensional space when $p$ is large, leading to a poor prediction of $f(x_{0})$ and a poor K-nearest neighbors regression fit.

As a general rule, parametric models will tend to outperform non-parametric models when there are only a small number of observations per predictor.

Next: Chapter 4 - Classification