stats-learning-notes

Chapter 4 - Classification

Though linear regression can be applied in the case of binary qualitative responses, difficulties arise beyond two levels. For example, choosing a coding scheme is problematic and different coding scheme can yield wildly different predictions.

Logistic Regression

Logistic regression models the probability that $y$ belongs to a particular category rather than modeling the response itself.

Logistic regression uses the logistic function to ensure a prediction between $0$ and $1 .$ The logistic function takes the form

$\normalsize p(X) = \frac{e^{\beta_{0} + \beta_{1}X}}{1 + e^{\beta_{0} + \beta_{1}X}} .$

This yields a probability greater than $0$ and less than $1 .$

The logistic function can be rebalanced to yield

$\normalsize \frac{p(X)}{1 - p(X)} = e^{\beta_{0} + \beta_{1}X}$

$\frac{p(X)}{1 - p(X)}$ is known as the odds and takes on a value between $0$ and infinity.

As an example, a probability of 1 in 5 yields odds of $\frac{1}{4}$ since $\frac {0.2}{1 - 0.2} = \frac{1}{4} .$

Taking a logarithm of both sides of the logistic odds equation yields an equation for the log-odds or logit,

$\normalsize \mathrm{log} \bigg \lgroup \frac{p(X)}{1 - p(X)} \bigg \rgroup = \beta_{0} + \beta_{1}X$

Logistic regression has a logit that is linear in terms of $X .$

Unlike linear regression where $\beta_{1}$ represents the average change in $Y$ with a one-unit increase in $X$ , for logistic regression, increasing $X$ by one-unit yields a $\beta_{1}$ change in the log-odds which is equivalent to multiplying the odds by $e^{\beta_{1}} .$

The relationship between $p(X)$ and $X$ is not linear and because of this $\beta_{1}$ does not correspond to the change in $p(X)$ given one-unit increase in $X$ . However, if $\beta_{1}$ is positive, increasing $X$ will be associated with an increase in $p(X)$ and, similarly, if $\beta_{1}$ is negative, an increase in $X$ will be associated with a decrease in $p(X)$ . How much change will depend on the value of $X$ .

Estimating Regression Coefficients

Logistic regression uses a strategy called maximum likelihood to estimate regression coefficients.

Maximum likelihood plays out like so: determine estimates for $\beta_{0}$ and $\beta_{1}$ such that the predicted probability of $\hat{p}(x_{i})$ corresponds with the observed classes as closely as possible. Formally, this yield an equation called a likelihood function:

$\normalsize \ell(\beta_{0}, \beta_{1}) = \displaystyle \prod_{i:y_{i}=1}p(X_{i}) \times \displaystyle \prod_{j:y_{j}=0}(1-p(X_{j})) .$

Estimates for $\beta_{0}$ and $\beta_{1}$ are chosen so as to maximize this likelihood function.

Linear regression’s least squares approach is actually a special case of maximum likelihood.

Logistic regression measures the accuracy of coefficient estimates using a quantity called the z-statistic. The z-statistic is similar to the t-statistic. The z-statistic for $\beta_{1}$ is represented by

$\normalsize \textrm{z-statistic}(\beta_{1}) = \frac{\hat{\beta}_{1}}{\mathrm{SE}(\hat{\beta}_{1})}$

A large z-statistic offers evidence against the null hypothesis.

In logistic regression, the null hypothesis

$\normalsize H_{0}: \beta_{1} = 0$

implies that

$\normalsize p(X) = \frac{e^{\beta_{0}}}{1 + e^{\beta_{0}}}$

and, ergo, $p(X)$ does not depend on $X .$

Making Predictions

Once coefficients have been estimated, predictions can be made by plugging the coefficients into the model equation

$\normalsize \hat{p}(X) = \frac{e^{\hat{\beta_{0}} + \hat{\beta_{1}}X}}{1 + e^{\hat{\beta}_{0} + \hat{\beta}_{1}X}} .$

In general, the estimated intercept, $\hat{\beta}_{0} ,$ is of limited interest since it mainly captures the ratio of positive and negative classifications in the given data set.

Similar to linear regression, dummy variables can be used to accommodate qualitative predictors.

Multiple Logistic Regression

Using a strategy similar to that employed for linear regression, multiple logistic regression can be generalized as

$\normalsize log \bigg \lgroup \frac{p(X)}{1 - p(X)} \bigg \rgroup = \beta_{0} + \beta_{1}X_{1} + \ldots + \beta_{p}X_{p}$

where $X = (X_{1}, X_{2}, \ldots, X_{p})$ are $p$ predictors.

The log-odds equation for multiple logistic regression can be expressed as

$\normalsize p(X) = \frac{e^{\beta_{0} + \beta_{1}X_{1} + \ldots + \beta_{p}X_{p}}}{1 + e^{\beta_{0} + \beta_{1}X_{1} + \ldots + \beta_{p}X_{p}}}$

Maximum likelihood is also used to estimate $\beta_{0}, \beta_{1}, \ldots, \beta_{p}$ in the case of multiple logistic regression.

In general, the scenario in which the result obtained with a single predictor does not match the result with multiple predictors, especially when there is correlation among the predictors, is referred to as confounding. More specifically, confounding describes situations in which the experimental controls do not adequately allow for ruling out alternative explanations for the observed relationship between the predictors and the response.

Logistic Regression For More Than Two Classes

Though multiple-class logistic regression is possible, discriminant analysis tends to be the preferred means of handling multiple-class classification.

Linear Discriminant Analysis

While logistic regression models the conditional distribution of the response $Y$ given the predictor(s) $X ,$ linear discriminant analysis takes the approach of modeling the distribution of the predictor(s) $X$ separately in each of the response classes , $Y$ , and then uses Bayes’ theorem to invert these probabilities to estimate the conditional distribution.

Linear discriminant analysis is popular when there are more than two response classes. Beyond its popularity, linear discriminant analysis also benefits from not being susceptible to some of the problems that logistic regression suffers from:

The parameter estimates for logistic regression can be surprisingly unstable when the response classes are well separated. Linear discriminant analysis does not suffer from this problem.
Logistic regression is more unstable than linear discriminant analysis when $n$ is small and the distribution of the predictors $X$ is approximately normal in each of the response classes.

Classification With Bayes’ Theorem

Assuming a qualitative variable $Y$ that can take on $K \geq 2$ distinct, unordered values, the prior probability describes the probability that a given observation is associated with the kth class of the response variable $Y .$

The density function of $X$ for an observation that comes from the kth class is defined as

$\normalsize f_{k}(X) = \mathrm{Pr}(X=x|Y=k) .$

This means that $f_{k}(X)$ should be relatively large if there’s a high probability that an observation from the kth class features $X = x .$ Conversely, $f_{k}(X)$ will be relatively small if it is unlikely that an observation in class k would feature $X = x .$

Following this intuition, Bayes’ theorem states

$\normalsize \mathrm{Pr}(Y=k|X=x) = p_{k}(x) = \frac{\pi_{k}f_{k}(X)}{\sum_{j=1}^{k}\pi_{j}f_{j}(X)}$

where $\pi_{k}$ denotes the prior probability that the chosen observation comes from the kth class. This equation is sometimes abbreviated as $p_{k}(x) .$

$p_{k}(x) = \mathrm{Pr}(Y=k|X)$ is also known as the posterior probability, or the probability that an observation belongs to the kth class, given the predictor value for that observation.

Estimating $\pi_{k},$ the prior probability, is easy given a random sample of responses from the population.

Estimating the density function, $f_{k}(X)$ tends to be harder, but making some assumptions about the form of the densities can simplify things. A good estimate for $f_{k}(X)$ allows for developing a classifier that approximates the Bayes’ classifier which has the lowest possible error rate since it always selects the class for which $p_{k}(x)$ is largest.

Linear Discriminant Analysis For One Predictor

When only considering one predictor, if we assume that $f_{k}(X)$ has a normal distribution, or Gaussian distribution, the normal density is described by

$\normalsize f_{k}(X) = \frac{1}{\sqrt{2\pi}\sigma_{k}}\exp \big \lgroup -\frac{1}{2\sigma_{k}^{2}}(x-\mu_{k})^{2} \big \rgroup$

where $\mu_{k}$ is the mean parameter for the kth class and $\sigma_{k}^{2}$ is the variable parameter for the kth class.

The density function can be further simplified by assuming that the variance terms, $\sigma_{1}^{2}, \ldots, \sigma_{k}^{2} ,$ are all equal in which case the variance is denoted by $\sigma^{2} .$

Plugging the simplified normal density function into Bayes’ theorem yields

$\normalsize p_{k}(x) = \frac{\pi_{k}\frac{1}{\sqrt{2\pi}\sigma}\exp \big \lgroup -\frac{1}{2\sigma^{2}}(x-\mu_{k})^2 \big \rgroup}{\sum_{j = 1}^{k} \pi_{j}\frac{1}{\sqrt{2\pi}\sigma}\exp \big \lgroup -\frac{1}{2\sigma^{2}}(x - \mu_{j})^2 \big \rgroup} .$

It can be shown that by taking a $\log$ of both sides and removing terms that are not class specific, a simpler equation can be extracted:

$\normalsize \delta_{k}(x) = \frac{x\mu_{k}}{\sigma^{2}} - \frac{\mu_{k}^{2}}{2\sigma^{2}} + \log(\pi_{k}) .$

Using this equation, an observation can be classified by taking the class yields the largest value.

Linear discriminant analysis uses the following estimated values for $\hat{\mu}_{k}$ and $\hat{\sigma}^{2} :$

$\normalsize \hat{\mu}_{k} = \frac{1}{n_{k}} \displaystyle \sum_{i:y_{i} = k} x_{i}$ $\normalsize \sigma^{2} = \frac{1}{n - k} \displaystyle \sum_{k=1}^{k} \displaystyle \sum_{i:y_{i} = k} (x_{i} - \mu_{k})^{2}$

where $n$ is the total number of training observations and $n_{k}$ is the number of training observations in class k.

The estimate of $\hat{\mu}_{k}$ is the average value of $x$ for all training observations in class k.

The estimate of $\hat{\sigma}^{2}$ can be seen as a weighted average of the sample variance for all k classes.

When the class prior probabilities, $\pi_{1}, \ldots, \pi_{k} ,$ is not known, it can be estimated using the proportion of training observations that fall into the kth class:

$\normalsize \hat{\pi}_{k} = \frac{n_{k}}{n}$

Plugging the estimates for $\hat{\mu}_{k}$ and $\hat{\sigma}_{k}^{2}$ into the modified Bayes’ theorem yields the linear discriminant analysis classifer:

$\normalsize \hat{\delta}_{k}(x) = \frac{x\hat{\mu}_{k}}{\hat{\sigma}^{2}} - \frac{\hat{\mu}_{k}^{2}}{2\hat{\sigma}^{2}} + \log(\hat{\pi}_{k})$

which assigns an observation $X = x$ to whichever class yields the largest value.

This classifier is described as linear because the discriminant function $\hat{\delta}_{k}(x)$ is linear in terms of $x$ and not a more complex function.

The Bayes decision boundary for linear discriminant analysis is identified by the boundary where $\delta_{k}(x) = \delta_{j}(x) .$

The linear discriminant analysis classifier assumes that the observations from each class follow a normal distribution with a class specific average vector and constant variance, $\sigma^{2}$ , and uses these simplifications to build a Bayes’ theorem based classifier.

Linear Discriminant Analysis with Multiple Predictors

Multivariate linear discriminant analysis assumes that $X = (X_{1}, X_{2}, \ldots, X_{p})$ comes from a multivariate normal distribution with a class-specific mean vector and a common covariance matrix.

The multivariate Gaussian distribution used by linear discriminant analysis assumes that each predictor follows a one-dimensional normal distribution with some correlation between the predictors. The more correlation between predictors, the more the bell shape of the normal distribution will be distorted.

A p-dimensional variable X can be indicated to have a multivariate Gaussian distribution with the notation $X \sim N(\mu, \Sigma)$ where $E(x) = \mu$ is the mean of $X$ (a vector with p components) and $\mathrm{Cov}(X) = \Sigma$ is the p x p covariance matrix of $X$ .

Multivariate Gaussian density is formally defined as

$\normalsize f(x) = \frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}} \exp \big \lgroup -\frac{1}{2}(x - \mu)^{T}\Sigma^{-1}(x - \mu) \big \rgroup .$

For linear discriminant analysis with multiple predictors, the multivariate Gaussian distribution, $N(\mu_{k}, \Sigma)$ , is assumed to have a class specific mean vector, $\mu_{k}$ , and a covariance vector common to all classes, $\Sigma .$

Combining the multivariate Gaussian density function with Bayes’ theorem yields the vector/matrix version of the linear discriminant analysis Bayes’ classifier:

$\normalsize \delta_{k}(x) = x^{T} \Sigma^{-1} \mu_{k} - \frac{1}{2} \mu_{k}^{T} \Sigma^{-1} \mu_{k} + \log \pi_{k}$

Again, whichever class yields the largest value is the highest probability classification.

The Bayes decision boundaries are defined by the values for which $\delta_{j}(x) = \delta_{k}(x)$ or more fully

$\normalsize x^{T} \Sigma^{-1} \mu_{j} - \frac{1}{2} \mu_{j}^{T} \Sigma^{-1}\mu_{j} = x^{T} \Sigma^{-1} \mu_{k} - \frac{1}{2} \mu_{k}^{T} \Sigma^{-1} \mu_{k}$

It should be noted that since all classes are assumed to have the same number of training observations, the $\log \pi$ terms cancel out.

As was the case for one-dimensional linear discriminant analysis, it is necessary to estimate the unknown parameters $\mu_{1}, \ldots, \mu_{k}$ , $\pi_{1}, \ldots, \pi_{k}$ , and $\Sigma .$ The formulas used in the multi-dimensional case are similar to those used with just a single dimension.

Since, even in the multivariate case, the linear discriminant analysis decision rule relates to $X$ in a linear fashion, the name linear discriminant analysis holds.

As with other methods, the higher the ratio of parameters, $p$ , to number of samples, $n$ , the more likely overfitting will occur.

In general, binary classifiers are subject to two kinds of error: false positives and false negatives. A confusion matrix can be a useful way to display these error rates. Class-specific performance is also important to consider because in some cases a particular class will contain the bulk of the error.

In medicine and biology, the term sensitivity refers to the percentage of observations correctly positively classified (true positives) and specificity refers to the percentage of observations correctly negatively classified (true negatives).

In a two-class scenario, the Bayes classifier, and by extension, linear discriminant analysis, uses a 50% threshold for the posterior probability when determining classifications. In some cases it may be desirable to lower this threshold.

A ROC curve is a useful graphic for displaying the two types of error rates for all possible thresholds. ROC is a historic acronym that comes from communications theory and stands for receiver operating characteristics.

Example ROC curve

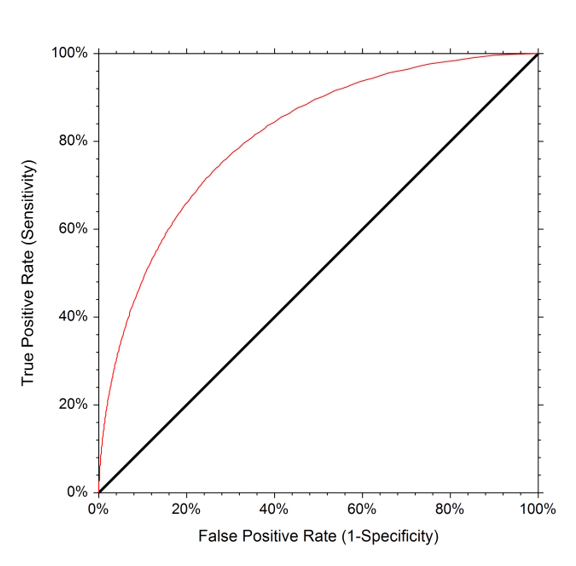
The overall performance of a classifier summarized over all possible thresholds is quantified by the area under the ROC curve.

A more ideal ROC curve will hold more tightly to the top left corner which, in turn, will increase the area under the ROC curve. A classifier that performs no better than chance will have an area under the ROC curve less than or equal to 0.5 when evaluated against a test data set.

In summary, varying the classifier threshold changes its true positive and false positive rate, also called sensitivity and $(1 - \mathrm{specificity}) .$

Quadratic Discriminant Analysis

Quadratic discriminant analysis offers an alternative approach to linear discriminant analysis that makes most of the same assumptions, except that quadratic discriminant analysis assumes that each class has its own covariance matrix. This amounts to assuming that an observation from the kth class has a distribution of the form

$\normalsize X \sim N(\mu_{k}, \Sigma_{k})$

where $\Sigma_{k}$ is a covariance matrix for class $k$ .

This yields a Bayes classifier that assigns an observation $X = x$ to the class with the largest value for

$\normalsize \delta_{k}(x) = - \frac{1}{2}(x - \mu_{k})^{T} \Sigma_{k}^{-1} (x - \mu_{k}) - \frac{1}{2} \log |\Sigma_{k}| + log \pi_{k}$

which is equivalent to

$\normalsize \delta_{k}(x) = - \frac{1}{2}x^{T} \Sigma_{k}^{-1} + x^{T} \Sigma_{k}^{-1}\mu_{k} - \frac{1}{2}\mu_{k}^{T} \Sigma_{k}^{-1} \mu_{k} - \frac{1}{2} \log | \Sigma_{k} | + \log \pi_{k} .$

The quadratic discriminant analysis Bayes classifier gets its name from the fact that it is a quadratic function in terms of $x .$

The choice between a shared covariance matrix (like that assumed in linear discriminant analysis) and a class-specific covariance matrix (like that assumed in quadratic discriminant analysis) amounts to a bias-variance trade-off. This is because when there are $p$ predictors, estimating a covariance matrix requires estimating $\frac{p(p + 1)}{2}$ parameters. Since quadratic discriminant analysis estimates a separate covariance matri for each class, this amounts to estimating $\frac{Kp(p + 1)}{2}$ parameters.

By assuming a common covariance matrix, linear discriminant analysis is linear in terms of $x$ which means $Kp$ linear coefficients must be estimated. Because of this, linear discriminant analysis is much less flexible than quadratic discriminant analysis, but as a result has much lower variance. If the assumption of a common covariance matrix is highly inaccurate, it can cause linear discriminant analysis to suffer from high bias.

In general terms, linear discriminant analysis tends to be a better choice if the importance of reducing variance is important because there are relatively few training examples. Conversely, quadratic discriminant analysis can be a better choice if the training set is large such that the variance of the classifier is not a concern or if the assumption of a common covariance matrix is not realistic.

Comparing Classification Methods

Since logistic regression and linear discriminant analysis are both linear in terms of $x ,$ the primary difference between the two methods is their fitting procedures. Linear discriminant analysis assumes that observations come from a Gaussian distribution with a common covariance matrix, and as such, out performs logistic regression in cases where these assumptions hold true.

K-nearest neighbors can outperform linear regression and linear discriminant analysis when the decision boundary is highly non-linear, but at the cost of a less interpretable model.

Quadratic discriminant analysis falls somewhere between the linear approaches of linear discriminant analysis and logistic regression and the non-parametric approach of K-nearest neighbors. Since quadratic linear analysis models a quadratic decision boundary, it has more capacity for modeling a wider range of problems.

Quadratic discriminant analysis is not as flexible as K-nearest neighbors, however it can perform better than K-nearest neighbors when there are fewer training observations due to its high bias.

Linear discriminant analysis and logistic regression will perform well when the true decision boundary is linear.

Quadratic discriminant analysis may give better results when the decision boundary is moderately non-linear.

Non-parametric approaches like K-nearest neighbors may give better results when the decision boundary is more complex and the right level of smoothing is employed.

As was the case in the regression setting, it is possible to apply non-linear transformations to the predictors to better accommodate non-linear relationships between the response and the predictors.

The effectiveness of this approach will depend on whether or not the increase in variance introduced by the increase in flexibility is offset by the reduction in bias.

It is possible to add quadratic terms and cross products to the linear discriminant analysis model such that it has the same form as quadratic discriminant analysis, however the parameter estimates for each of the models would be different. In this fashion, it’s possible to build a model that falls somewhere between linear discriminant analysis and quadratic discriminant analysis.

Next: Chapter 5 - Resampling Methods